Længde af graf
Hvis grafen for en funktion er en ret linje, kan vi til hver en tid – med Pythagoras – beregne længden af grafen. For andre grafer må vi tage integralregning i brug.
For længden af kurver, hvor x- og y-koordinaterne er givet ved en parameterfremstilling, henvises til afsnittet om vektorfunktioner.
Her kigger vi på grafer for funktioner, hvor y er beskrevet som en funktion af x. For at komme frem til en formel for grafens længde, betragter vi først et lille stykke af grafen med udbredelsen dx i x-retningen og dy i y-retningen, se figur 1.
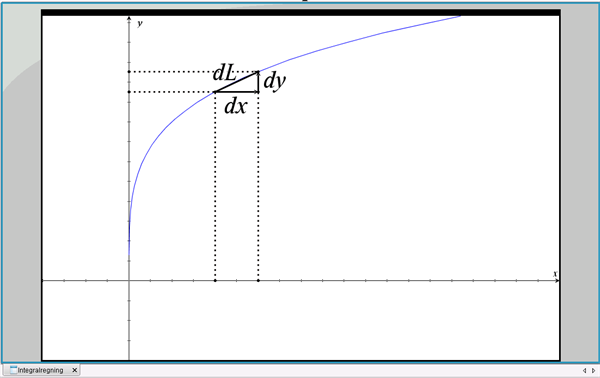
Figur 1 Bestemmelse af infinitesimalt bidrag til længden af en graf
Ved at bruge Pythagoras finder vi: \( dL^2 = dx^2+dy^2\).
Vi omskriver til \(dL = \sqrt{dx^2+dy^2}\), og i det sidste led under kvadratroden dividerer og ganger vi med \(dx^2\): \(dL= \sqrt{dx^2+\frac{dy^2}{dx^2}dx^2}\).
Vi benytter omskrivningen: \(\frac{dy^2}{dx^2} = (\frac{dy}{dx})^2\) og får: \(dL= \sqrt{dx^2+(\frac{dy}{dx})^2\cdot dx^2}\). Nu indgår \(dx^2\) i begge led under kvadratroden, så vi kan sætte \(dx^2\) udenfor en parentes: \(dL= \sqrt{(1+(\frac{dy}{dx})^2)\cdot dx^2}\).
Vi deler kvadratroden op: \(dL= \sqrt{1+(\frac{dy}{dx})^2} \cdot \sqrt{\:dx^2} = \sqrt{1+(\frac{dy}{dx})^2} \cdot dx \) \(=\sqrt{1+f'(x)^2} \cdot dx\)
Vi har forudsat, at grafen er differentiabel og har indsat \(\frac{dy}{dx}=f’(x)\).
Længden af grafen kan vi nu bestemme ved at integrere udtrykket for \(dL\) over det ønskede x-interval:
\(\displaystyle L = \int_{}^{} \: dL = \int_{x_1}^{x_2} \sqrt{1+f'(x)^2} \:dx\)
OBS: Denne formel er rigtig, men udledningsmetoden er ikke stringent, da man ser dx og dy som selvstændige matematiske objekter. I anden del af videolektionen i bunden af siden kan du se en stringent udledning.
Eksempel 1
En mand skal bevæge sig fra punkt A til punkt B. Afstanden i fugleflugtslinje mellem punkterne betegner vi \(d\). Uvist af hvilke grunde er manden ikke i stand til at følge den rette linje, i stedet viser det sig, at hans rute svarer præcist til én periode på en sinuskurve med amplituden \(a\) i forhold til fugleflugtslinjen. Se figur 2.
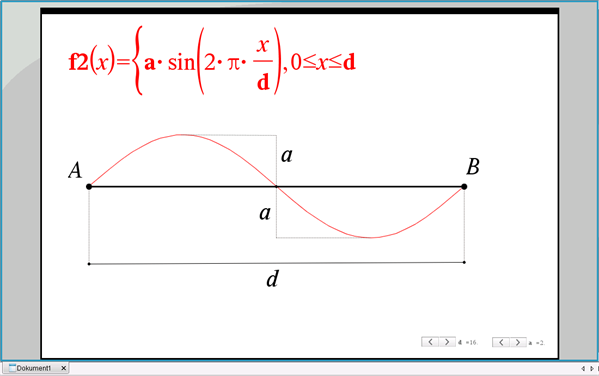
Figur 2 Bevægelse fra A til B i en sinuskurve
Sinuskurven beskrives ved funktionen \(f(x) = a\cdot\sin (2\pi\frac{x}{d})\), \(0\leq x\leq d\). For at beregne længden af sinuskurven skal vi bruge \(f’(x) = 2\pi \cdot\frac{a}{d}\cdot\cos (2\pi\frac{x}{d})\), og længden af sinuskurven beregnes ved hjælp af integralet:
\(\displaystyle L = \int_{0}^{d}\sqrt{1+f’(x)^2}\: dx = \int_{0}^{d}\sqrt{1+4\pi ^2\cdot (\frac{a}{d})^2\cdot\cos^2(2\pi \frac{x}{d})}\: dx\)
Her indfører vi substitutionen \(z = \frac{x}{d}\) og \(dx = d\cdot dz\), hvor \(z_1 = 0\) og \(z_2 = 1\):
\(\displaystyle L = d\cdot\int_{0}^{1}\sqrt{1+4\pi ^2\cdot (\frac{a}{d})^2\cdot\cos^2(2\pi z)}\: dz\)
Længden beregnes altså som afstanden i fugleflugtslinje \(d\) ganget med integralet, og integralet ses kun at være afhængigt af forholdet mellem amplituden \(a\) og afstanden \(d\). Integralet giver os derfor en talværdi for, hvor meget sinuskurven er længere end afstanden målt i fugleflugtslinje som funktion af forholdet mellem amplituden \(a\) og afstanden \(d\).
Integralet kan beregnes i CAS med forskellige værdier af forholdet mellem amplituden \(a\) og afstanden \(d\) indsat. Nogle resultater er gengivet her:
| Forholdet \(\frac{a}{d}\) | Længde af sinuskurve |
| 0,1 = 10 % | \(d\cdot 1,09\) |
| 0,2 = 20 % | \(d\cdot 1,32\) |
| 0,3 = 30 % | \(d\cdot 1,65\) |
Det ses, at sinuskurvens længde vokser relativt hurtigt. Hvis sinuskurvens amplitude udgør 10 % af afstanden \(d\) mellem A og B, er sinuskurven 9 % længere end \(d\). Men hvis sinuskurvens amplitude stiger til 20 % af \(d\), er sinuskurven 32 % længere end \(d\), og ved en amplitude på 30 % af \(d\), er sinuskurven hele 65 % længere end \(d\).
Eksempel 2
En vej skal anlægges mellem to punkter A og B, se figur 3. Pythagoras giver, at afstanden mellem A og B er 10 km: \(a^2+b^2 = 8^2 + 6^2 = 100 = c^2 = 10^2\).
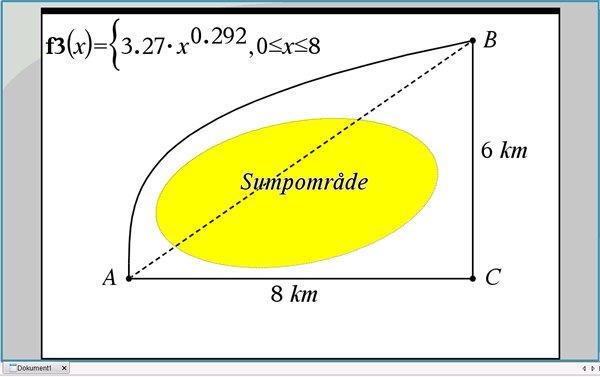
Figur 3 Linjeføring af vej mellem A og B
På grund af et sumpområde på strækningen kan vejen ikke anlægges som en ret linje. Jordbundsundersøgelser har kortlagt sumpområdets udstrækning, og det har vist sig, at vejen kan anlægges enten langs en nordlig linjeføring beskrevet ved potensvækst-funktionen \(f(x) = b\cdot x^a = 3,27\cdot x^{0,292}\), eller som to rette linjer hhv. fra A til C og fra C til B.
Beregn forskellen i længde mellem de to linjeføringer.
Vi ser først, at linjeføringen som to rette linjer giver en længde på 8 + 6 = 14 km.
For linjeføringen beskrevet ved \(f(x)\) skal vi differentiere funktionen: \(f’(x) = b\cdot a\cdot x^{a-1} = 3,27\cdot 0,292\cdot x^{-0,708} = 0,955\cdot x^{-0,708}\) og længden af linjeføringen beregnes ved hjælp af integralet:
\(\displaystyle L = \int_{0}^{8}\sqrt{1+f’(x)^2}\: dx = \int_{0}^{8}\sqrt{1+0,955^{2}\cdot x^{-2\cdot 0,708}}\: dx\)
Integralet beregnes i CAS og giver, at \(L\) er 11,1 km.
Forskellen i vejlængde mellem de to linjeføringer er altså 14 - 11,1 = 2,9 km.
