Konstruktion af midtnormal
En midtnormal for et linjestykke (\(AB\)) er en linje, der står vinkelret på linjestykket og deler linjestykket på midten, dvs. i to lige store dele, se figur 1.
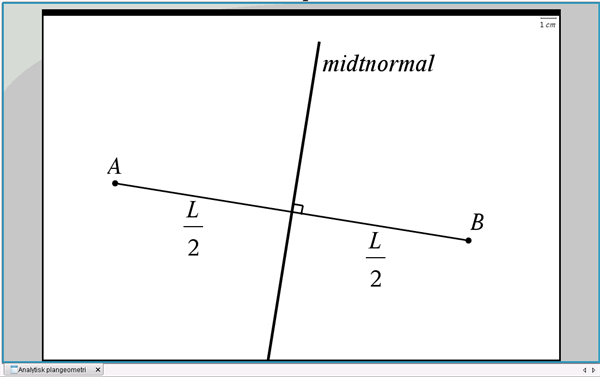
Figur 1 Midtnormalen for et linjestykke
Midtnormalen kan også opfattes som en symmetrilinje (spejlingsakse) for linjestykket. Derudfra kan vi udlede en vigtig egenskab ved midtnormalen: Ethvert punkt på midtnormalen ligger lige langt fra linjestykkets to endepunkter \(A\) og \(B\).
For at kunne tegne midtnormalen har vi brug for at fastlægge to punkter på den – f.eks. et punkt over linjestykket og et punkt under linjestykket. Da punkter på midtnormalen har samme afstand til punkt \(A\) og punkt \(B\), kan vi løse opgaven i følgende tre simple trin, se figur 2:
- tegn en cirkel med centrum i punkt \(A\) og radius \(AB\) (dvs. denne cirkel går gennem punkt \(B\))
- tegn en cirkel med centrum i punkt \(B\) og radius \(AB\) (dvs. denne cirkel går gennem punkt \(A\))
- tegn en linje gennem de to cirklers to skæringspunkter – denne linje er midtnormal for linjestykket \(AB\).
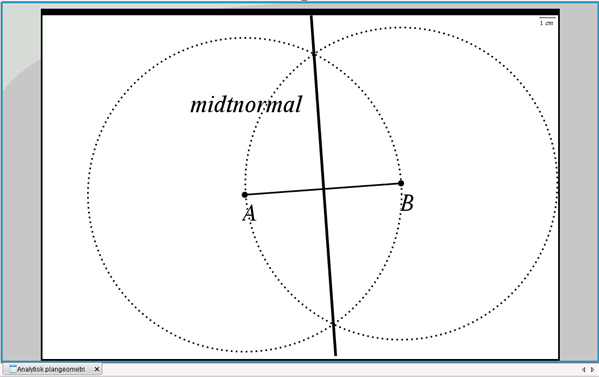
Figur 2 Konstruktion af midtnormalen for et linjestykke
Bemærk: Cirklerne i de to første trin skal ikke nødvendigvis have radius \(AB\). Du kan benytte en anden radius, men radius skal være den samme i begge cirkler, og radius skal være større end halvdelen af \(AB\).
Når man konstruerer midtnormalen manuelt på papir med brug af en passer og en lineal, opnår man en hensigtsmæssig nøjagtighed ved at bruge \(AB\) som radius i cirklerne. Hvis man benytter en radius, der kun er lidt større end halvdelen af \(AB\), vil en lille fejlplacering af passeren kunne resultere i en forholdsvis stor afvigelse set i forhold til, om man opnår en ret vinkel mellem midtnormalen og linjestykket.
Når man konstruerer midtnormalen med et IT-værktøj, har størrelsen af radius i cirklerne derimod ingen praktisk betydning for nøjagtigheden - den skal bare være større end halvdelen af \(AB\).
