Dobbeltlogaritmisk koordinatsystem
Efter at have set på de to typer enkeltlogaritmiske koordinatsystemer, kan vi analysere spejlingen af punktområder i det sædvanlige (x,y)-koordinatsystem til en ny position i det dobbelt-logaritmiske koordinatsystem med logaritmisk skala på både x- og y-aksen.
Idet logaritmen stadig kun er defineret for positive parametre, kan kun punkter med både positiv x-værdi og positiv y-værdi, dvs. 1. kvadrant i det sædvanlige (x,y)-koordinatsystem, spejles til punkter i det dobbelt-logaritmiske koordinatsystem.
Vi bemærker videre, at punktet P (1,1) i det sædvanlige (x,y)-koordinatsystem spejles over i Origo (0,0) i det dobbelt-logaritmiske koordinatsystem, idet både Log(x=1) = 0 og Log(y=1) = 0.
Hvis vi inddeler 1. kvadrant i det sædvanlige (x.y)-koordinatsystem i 4 områder (A1, B1, C1, D1) som vist øverst i figur 4, bliver disse spejlet over i de 4 kvadranter (A2, B2, C2, D2) i det dobbelt-logaritmiske koordinatsystem, som vist nederst i figur 4:
| (x.y)-koordinatsystem | Dobbelt-logaritmisk koordinatsystem | |||
| A1: | x ≥ 1, y ≥ 1 | A2: | Log(x) ≥ 0, Log(y) ≥ 0 | |
| B1: | 0 < x ≤ 1, y ≥ 1 | B2: | Log(x) ≤ 0, Log(y) ≥ 0 | |
| C1: | 0 < x ≤ 1, 0 < y ≤ 1 | C2: | Log(x) ≤ 0, Log(y) ≤ 0 | |
| D1: | x ≥ 1, 0 < y ≤ 1 | D2: | Log(x) ≥ 0, Log(y) ≤ 0 | |
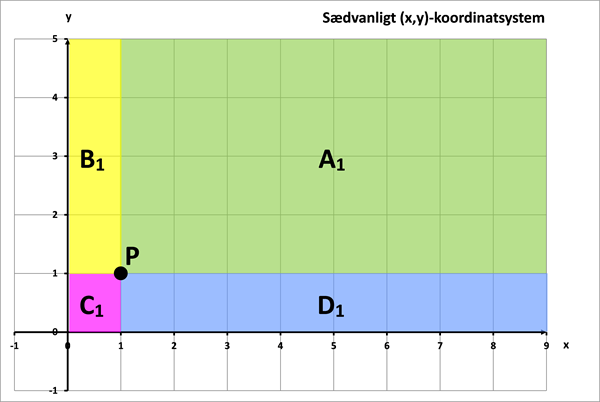
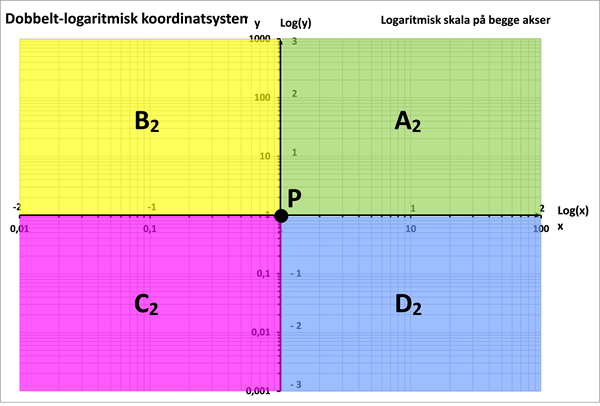
Figur 4 Spejling af punktområder i det sædvanlige (x,y)-koordinatsystem (øverst) til et dobbelt-logaritmisk koordinatsystem med logaritmisk skala på begge akser (nederst)
Punkter på y-aksen i det sædvanlige (x,y)-koordinatsystem er ikke med i hverken B1 eller C1, og punkter på x-aksen i det sædvanlige (x,y)-koordinatsystem er ikke med i hverken C1 eller D1, da disse punkter (med hhv. x-værdien 0 og y-værdien 0) ikke kan spejles til det dobbelt-logaritmiske koordinatsystem.
For en god ordens skyld bemærker vi, at logaritmen til meget små, men positive, såvel x-som y-værdier uendelig tæt på nul er store negative tal. Vi formulerer det matematisk som \(lim_{x\to 0^+} Log(x) = -\infty\) og \(lim_{y\to 0^+} Log(y) = -\infty\).
Anvendelse
Også i arbejdet med potensvækstmodeller kan vi i et sædvanligt (x,y)-koordinatsystem med en lineær skala på y-aksen være tvunget til at vælge enten en skala, der er velegnet for aflæsning af funktionsværdien ved små x-værdier, eller en skala, der er velegnet for aflæsning af funktionsværdien ved større x-værdier. Her kan et dobbelt-logaritmisk koordinatsystem hjælpe os.
En potensvækstmodel har forskriften:
\(f(x) = b\cdot x^a\), hvor \(b > 0\) og \(x > 0\)
Hvis vi beregner logaritmen på begge sider af lighedstegnet, får vi ved brug af regnereglerne for logaritmer:
\(Log(f(x)) = Log(b\cdot x^a) = Log(b) + Log(x^a)\) og dermed
\(Log(f(x)) = Log(b) + a\cdot Log(x) = a\cdot Log(x) + Log(b)\)
hvor \(b > 0\) og \(x > 0\).
Vi genkender højresiden som forskriften for en ret linje, hvor skæringen med y-aksen er Log(\(b\)) og hældningen er \(a\). Vi kan altså konkludere, at hvis vi afbilder logaritmen til \(f(x)\) som funktion af logaritmen til \(x\), er resultatet en ret linie.
Og så er det jo netop det dobbelt-logaritmiske koordinatsystem, hvor vi har en logaritmisk skala på både y-aksen og x-aksen, der kommer i spil.
Eksempel
Vi vil afbilde potensvækstmodellen \(f(x) = 2,0\cdot x^{1,35}\), hvor \(x\ge 0\).
Hvis vi vil kunne aflæse y-værdierne for x-værdier op til 100, kan vi afbilde funktionen i et sædvanligt (x,y)-koordinatsystem med en y-akse gående fra 0 til 1000, som vist i det midterste diagram i figur 6. Men her er det mere end vanskeligt at aflæse y-værdierne for x-værdier under 20. Hvis vi med rimelig nøjagtighed vil kunne aflæse y-værdierne for x-værdier under 20, kan vi afbilde funktionen i et sædvanligt (x,y)-koordinatsystem med en y-akse gående fra 0 til 120, som vist i det øverste diagram i figur 6.
I det dobbelt-logaritmiske koordinatsystem nederst i figur 6 kan vi se, at funktionen som forventet afbildes som en ret linje, og vi kan med rimelig nøjagtighed aflæse y-værdierne i hele x-intervallet fra 0 til 100.
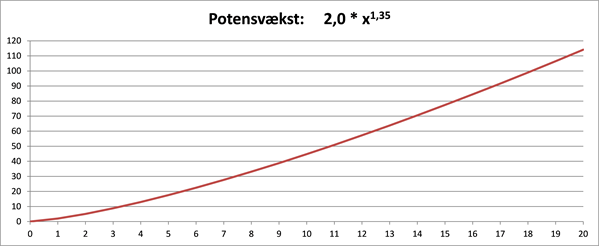
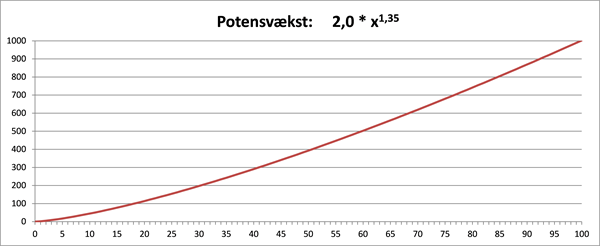
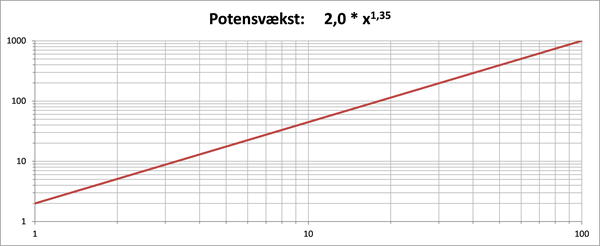
Figur 6 Potensvækstmodel vist i det sædvanlige (x,y)-koordinatsystem (øverst og i midten med forskellig skalering på akserne) og i et dobbelt-logaritmisk koordinatsystem med logaritmisk skala på begge akser (nederst)
