Integration ved substitution

Man kan differentiere alle differentiable funktioner. Der findes en række regler, og hvis man følger dem til punkt og prikke, kan man finde frem til den rigtige differentialkvotient. Det er ikke helt lige så let at integrere. Så snart man skal integrere et produkt af funktioner eller en sammensat funktion, er der ikke nogen klare regler, man bare kan følge slavisk. I stedet findes der en del forskellige metoder, man kan bruge til at omskrive integralet til noget, der er lettere at have med at gøre. Det er ikke altid til at sige, om den ene eller den anden metode vil virke; man må prøve sig frem.

En af de vigtigste metoder til integration er integration ved substitution.

Hvornår kan integration ved substitution bruges?

Når integranden (indmaden i integralet) indeholder et produkt af funktioner, og når en af dem er sammensat. Det er ikke i alle disse tilfælde, det vil virke, men ofte er det et forsøg værd.

Hvad er integration ved substitution?

Integration ved substitution er egentlig følgende formler

$$\int f(g(x))\cdot g'(x)\:dx=\int f(t)\:dt$$

$$\int_a^b f(g(x))\cdot g'(x)\:dx=\int_{g(a)}^{g(b)} f(t)\:dt,\qquad\text{hvor }t=g(x)$$

Formlerne ser meget uoverskuelige ud. Imidlertid er metoden ikke så vanskelig i praksis. Vi illustrerer den ved hjælp af nogle eksempler.

Vi ønsker at udregne følgende integral

$$\int x\cdot e^{x^2}\:dx$$

Vi ser, at der både er tale om et produkt af funktioner, og at den ene er sammensat. Derfor prøver vi os frem med integration ved substitution.

Det første, man gør, er at finde den indre funktion i den sammensatte funktion.
I vores tilfælde er det x². Vi kalder den indre funktion for t.

$$t=x^2$$

Nu differentierer vi t:

$$\frac{dt}{dx}=2x$$

venstresiden er bare et symbol, der betyder, at vi har differentieret t med hensyn til variablen x. 

Imidlertid lades vi som om, at symbolet er en brøk og isolerer dx.

$$dx=\frac{1}{2x}dt$$

Nu sætter vi t ind i integralet samt det nye udtryk for dx.

$$\int x\cdot e^{x^2}\:dx=\int x\cdot e^t\cdot\frac{1}{2x}\:dt$$

Til sidst skal vi reducere integranden, og udføre integrationen.

$$\int x\cdot e^t\cdot\frac{1}{2x}\:dt=\int \frac{1}{2}e^t\:dt=\frac{1}{2}e^t+c$$

Som rosinen i pølseenden substituerer vi den indre funktion tilbage ind på t's plads.

$$\int x\cdot e^{x^2}\:dx=\frac{1}{2}e^{x^2}+c$$

Opsamling

• Find den indre funktion og kald den t
• Differentier t, dvs. find dt/dx
• Isolér dx
• Indsæt nu t samt udtrykket for dx i integralet
• Tilbage-substituer den indre funktion på t's plads.

Hvis der er tale om et bestemt integral, skal man huske at integrationsgrænserne også skal substitueres.

Lad os regne følgende eksempel med et bestemt integral

$$\int_0^{\frac{\pi}{2}} (\sin(x))^3\cos(x)\:dx$$

Vi ser, at sin(x) er den indre funktion.

$$t=\sin(x)$$

Vi differentierer t.

$$\frac{dt}{dx}=\cos(x)$$

Vi lades som om symbolet til venstre er en brøk, og isolerer dx.

$$dx=\frac{1}{\cos(x)}dt$$

Nu skal vi finde de nye integrationsgrænser. Det gør vi ved at sætte de gamle grænser ind i den funktion, vi substituerer ud (i vores tilfælde sin(x)).

$$\sin(0)=0$$

$$\sin(\frac{\pi}{2})=1$$

Nu sætter vi t og udtrykket for dx samt de nye grænser, ind i integralet

$$\int_0^{\frac{\pi}{2}}(\sin(x))^3\cdot\cos(x)\:dx=\int_0^1t^3\cdot\cos(x)\cdot\frac{1}{\cos(x)}\:dt$$

Vi ser, at cos(x)'erne går ud med hinanden.

$$\int_0^1t^3\cdot\cos(x)\cdot\frac{1}{\cos(x)}\:dt=\int_0^1t^3\:dt=\left[\frac{1}{4}t^4 \right ]_0^1=\frac{1}{4}\cdot1^4-\frac{1}{4}\cdot0^4=\frac{1}{4}$$

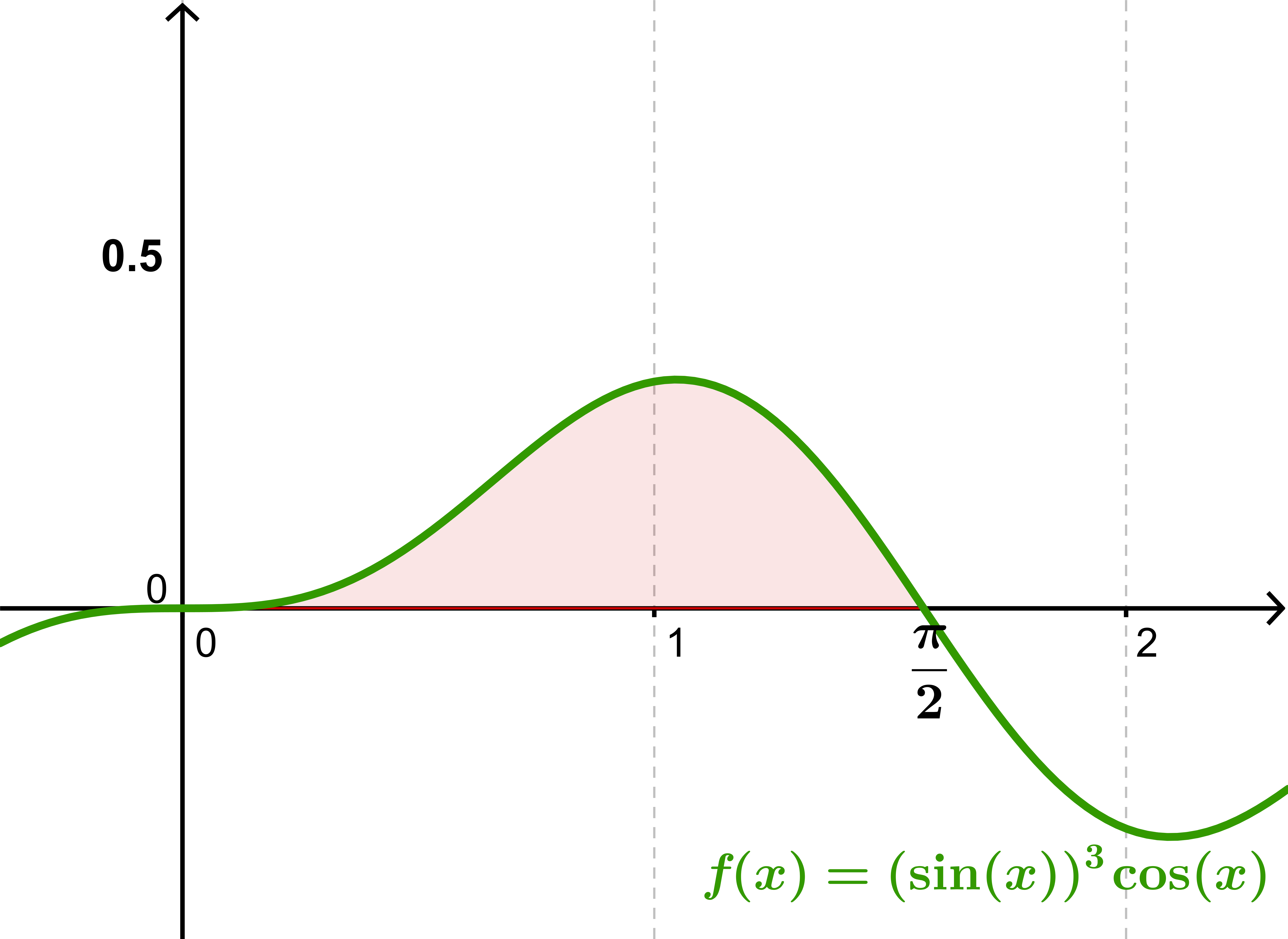
Arealet markeret på figuren er altså ¼.

---

Videolektion