Parameterfremstillingen for en elipse

Vi forestiller os en partikel, der gennemløber en ellipse­formet bane, idet ellipsen har centrum i (0,0), storakse \(a\) i x-aksens retning og lilleakse \(b\) i y-aksens retning. I figur 7 er vist et eksempel, hvor \(a=3\) og \(b=2\).

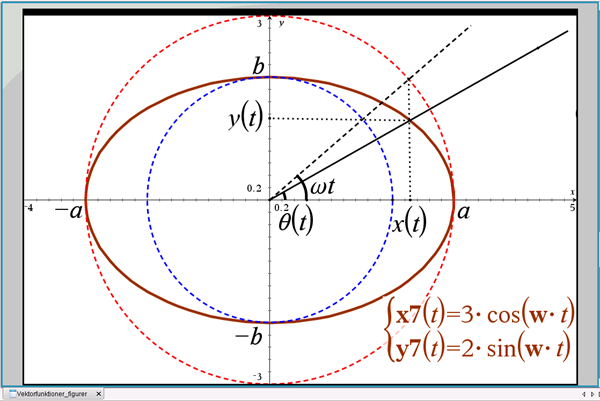
Figur 7      Parameterfremstilling for en ellipse 

På figuren er også indtegnet ”storcirklen” med radius \(a=3\) og ”lillecirklen” med radius \(b=2\).

Vi ser, at koordinaterne til et punkt \((x(t), y(t))\) i den ellipse­formede bane svarer til hhv. x-koordinaten i storcirklen og y-koordinaten i lillecirklen, begge hørende til en vinkeldrejning \(\omega\cdot t\), hvor \(\omega\) (rad/sek) betegner den gennemsnit­lige vinkel­hastighed i ellipsebanen, og omløbstiden er \(T=\frac{2\pi}{\omega}\):

       \(\overrightarrow{r(t)}=(x(t),y(t))=(a\cdot \cos(\omega t), b\cdot \sin(\omega t))\), \(0\leq t\leq \frac{2\pi}{\omega}\)

(hvor definitions­mængden for \(t\) her igen er afgrænset svarende til ét fuldt gennemløb).

I figur 7 har vi med \(\theta (t)\) angivet vinklen fra x-aksen til sted­vektoren til partiklen i ellipsebanen, og her gælder:

       \(\tan(\theta (t))=\dfrac{y(t)}{x(t)}=\dfrac{b  \cdot  \sin(\omega t)}{a  \cdot  \cos(\omega t)}=\dfrac{2}{3}\cdot \tan(\omega t)\), \(0\leq t\leq \frac{2\pi}{\omega}\).

I figur 8 er vist grafen for \(\theta (t)\) som funktion af tiden. Det fremgår, at vinkelhastig­heden (aflæses som grafens hældning) i en ellipsebane ikke er konstant. Den er nemlig størst omkring lilleaksens poler og mindst omkring storaksens poler.

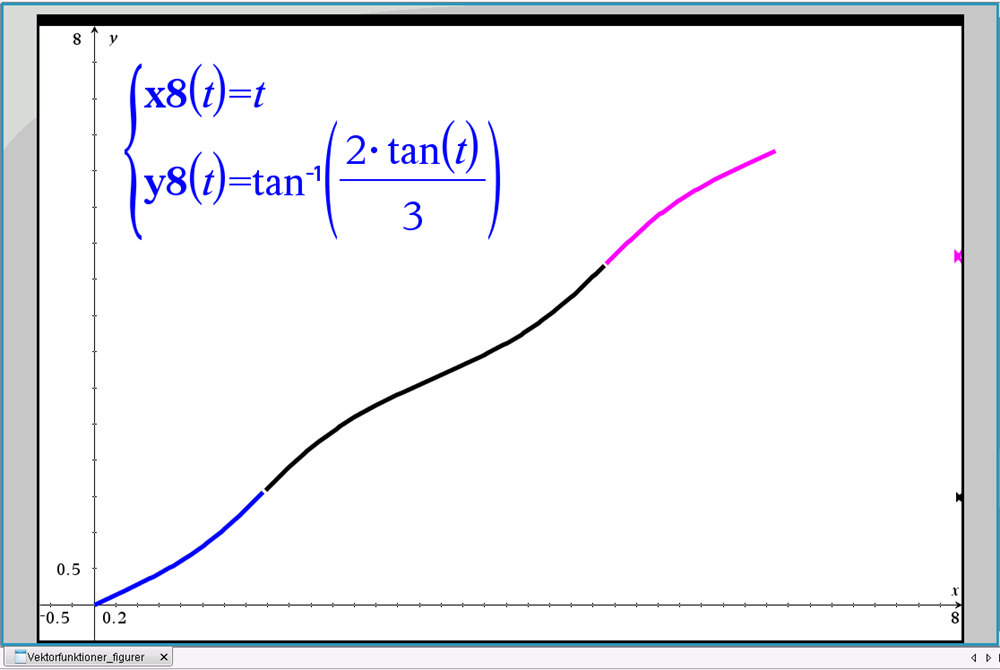
Figur 8      Vinkelhastigheden varierer i en elliptisk banekurve