Konfidensintervaller
Hvis vi ønsker at bestemme middelværdien for højden af alle gymnasieelever i Danmark, kan vi fx udvælge en 1.g-klasse i Københavnsområdet og beregne middelværdien for de studerendes højde i denne klasse.
Den beregnede middelværdi er så et estimat for middelværdien for højden for alle gymnasieelever i Danmark. Hvis vi nu vælger en anden klasse og igen beregner middelværdien, så får vi et andet estimat for middelværdien.
Dette estimat ligger sikkert tæt på den første beregnede middelværdi uden at være identisk med denne. Vi kalder det at udvælge en gymnasieklasse for tage en stikprøve ud af den samlede population bestående af samtlige gymnasieelever i Danmark.
Stikprøvens middelværdi kaldes også for et punktestimat for populationens middelværdi. Men hvis to forskellige stikprøver giver to forskellige estimater for middelværdien, hvordan kan vi så stole på estimatet? Hvad nu hvis vi i stedet for bare et enkelt punktestimat kunne bestemme et interval, som med stor sandsynlighed indeholder den rigtige ukendte middelværdi for hele populationen?
Et sådan interval kaldes også for et konfidensinterval. Et konfidensinterval er kendetegnet ved et niveau \(1 - \alpha\) og en typisk værdi for \(\alpha\) er \(5\%\), hvor man så taler om et \(1-\alpha = 95\%\)-konfidensinterval.
Formel
Hvis vi antager, at gymnasieelevers højde er normalfordelt med ukendt middelværdi \(\mu\) og en kendt spredning på \(\sigma\), så er formlen for et \(95\%\)-konfidens\-interval
\begin{equation}
95\%\mbox{-konfidensinterval} = \Big[\bar{x} - 1,96⋅\frac{\sigma}{\sqrt{n}};
\bar{x} +1,96⋅\frac{\sigma}{\sqrt{n}} \Big],
\end{equation}
hvor
- \(\bar{x}\) er stikprøvens middelværdi og
- \(n\) er stikprøvens størrelse.
Vi vender tilbage til konstanten \(1{,}96\).
Eksempel
Hvis vi antager at gymnasieelevers højde er tilnærmelsesvist normalfordelt med ukendt middelværdi \(\mu\) og standard afvigelse på \(\sigma=10\mbox{cm}\), og vi har følgende stikprøve på 27 elevers højde (målt i cm)
\begin{align*}
&175, 161, 177, 173, 179, 174, 173, 184, 184, 170, 169, 175, 175, 186, \\
&169, 169, 176, 166, 181, 175, 179, 179, 183, 166, 179, 160, 170
\end{align*}
så kan vi beregne stikprøvens middelværdi til 174,33 og derfor er \(95\%\)-konfidensintervallet bestemt ved
\(\Big[174,33 - 1,96 \frac{10}{\sqrt{27}}; 174,33 + 1,96 \frac{10}{\sqrt{27}} \Big]\)
\begin{align*}
&=\Big[174,33 - 3,77 ; 174,33 + 3,77 \Big] \\&= \Big[ 170,56; 178,10\Big]
\end{align*}
Konstanten 1,96
Hvor kom konstanten 1,96 fra som indgik i formlen for \(95\%\)-konfidensintervallet? Hvis vi kigger for fordelingsfunktionen for en normalfordeling med middelværdi 0 og varians 1, så er det samlede areal under kurven 1. Hvis vi derfor er interesseret i at finde det område under grafen, som dækker 95% af arealet, skal vi altså fjerne 2,5% af arealet i begge ender.
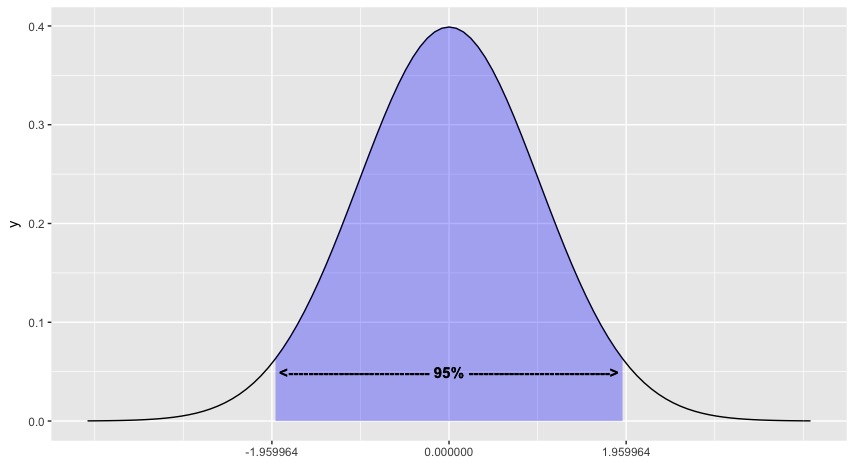
De \(\pm 1,96\) svarer præcis til det område under kurven som giver en areal
på 95%. Andre ofte anvendte konfidensintervaller er angivet i denne tabel.
| Konfidensniveau | konstant |
| 68% | 1 |
| 90% | 1,645 |
| 95% | 1,96 |
| 99% | 2,58 |
Hvis man skal regne fx et 90% konfidensinterval skal konstanten 1,96 erstattes med 1,645.
Får man brug for at bestemme andre konstanter kan man bruge Microsoft Office Excel til at udregne disse. Skal man bestemme et 92% konfidensinterval kan man finde konstanten med funktionen NORMSINV i Excel. Her skal man så udregne \(1-\alpha = 0,92\) så \(\alpha = 0,08\) og herefter indsætter man
\begin{equation}
\mbox{NORMSINV} \Big( 1-\frac{0,08}{2} \Big) = 1,75
\end{equation}
Bruger man den danske version af Excel, hedder funktionen STANDARD.NORM.INV. Matlab fra MathWorks har tilsvarende funktionalitet. Her bruger man funktionen norminv
\begin{equation}
\mbox{norminv}\big([0.04; 0.96], 0, 1\big),
\end{equation}
hvor 0 angiver middelværdien og 1 variansen.
Konfidensinterval for binominalfordelinger
Ved en rundspørge på et gymnasie har 62 af 1.g. elever sagt, at de var tilfredse
med introduktionsforløbet. 29 elever svarede, at de ikke var tilfredse.
Hvordan bestemmer man et \(95\%\)-konfidens-interval for andelen af tilfredse
elever? Hvis \(X\) er antallet af elever som er tilfredse med introduktionsforløbet
ud af en stikprøve på 62 + 29 = 91, så er X binominalfordelt
\(X \sim b\big(n=91,p \big)\)
Vi har her en fast med ukendt sandsynlighed for at der bliver succes. Denne
paramater kaldes sandsynlighedsparameteren og betegnes \(p\).
Sandsynlighedsparameteren kan estimeres til \(\widehat{p}\)
\begin{equation}
\widehat{p} = \frac{62}{91} = 0,68
\end{equation}
Dette er en approksimation af \(\widehat{p}\), der kun gælder når stikprøven er tilpas stor, og når \(p\) ikke er meget lille eller meget stor.
Formel
Formlen for et \(95\%\)-konfidens-interval i binominalfordelingen er
\begin{equation}
\Bigg[ \widehat{p} - 1,96 \sqrt{\frac{\widehat{p}\big(1-\widehat{p}\big)}{n}} ;
\widehat{p} + 1,96 \sqrt{\frac{\widehat{p}\big(1-\widehat{p}\big)}{n}} \Bigg]
\end{equation}
Indsætter vi i denne formel findes konfidensintervallet
$$ \Bigg[ 0,68 - 1,96 \sqrt{\frac{0,68\big(1-0,68\big)}{n}} ;
0,68 + 1,96 \sqrt{\frac{0,68\big(1-0,68\big)}{n}} \Bigg] $$
$$ = \Big[0,58 ; 0,78 \Big] $$
Altså vil tilfredsheden med introforløbet med 95% sikkerhed være mellem 58% og 78%.
