Dobbeltpunkt

Et dobbeltpunkt for en vektorfunktion er et punkt, hvor den tilhørende kurve skærer sig selv. (Vi medregner ikke kurver, der gennemløbes flere gange, hvor alle punkter på kurven kan siges at være et dobbelt­punkt.)

For at undersøge om parameterfremstillingen for en vektor­funktion indeholder et eller flere dobbeltpunkter, skal vi altså søge løsninger til ligningssystemet:

\(\overrightarrow{r(t_2)}=\overrightarrow{r(t_1)}\)        eller           \(x(t_2)=x(t_1)\) og \(y(t_2)=y(t_1)\)

Eksempel

Der er givet følgende vektorfunktion (\(t\) angiver radianer):

\(\overrightarrow{r(t)}=(x(t), y(t)) = (4\cdot\cos(t), 4-t-2\cdot\sin(3t))\)

I figur 10 er tegnet en del af kurven, der starter ved \(t=0\) i \((x,y)=(4,4)\). Bestem koordinaterne til parameter­frem­stil­lingens første dobbeltpunkt.

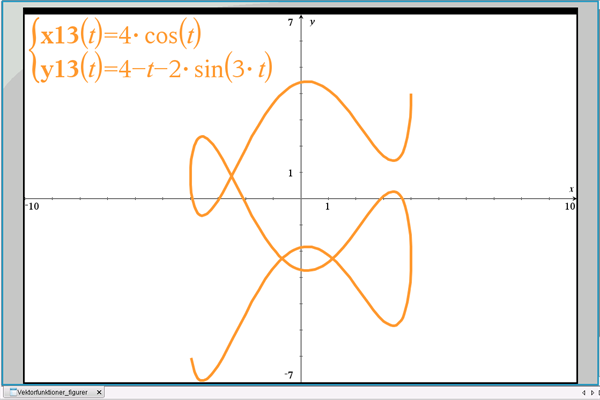
Figur 10    Dobbeltpunkter for en vektorfunktion er punkter, hvor kurven skærer sig selv

Betingelsen \(x(t_2)=x(t_1)\) giver, at \(\cos(t_2)=\cos(t_1)\). Denne ligning har flere (uendeligt mange) løsninger, men vi er her kun interesserede i den første: \(t_2=2\pi-t_1\), som indsættes i \(y(t_2)=y(t_1)\):

\(4-(2\pi-t_1)-2\cdot\sin(6\pi-3t_1)=4-t_1-2\cdot\sin(3t_1)\)

Denne ligning omformes til: \(2\cdot t_1-2\pi+4\cdot\sin(3t_1)=0\), som løses i et værktøjsprogram: \(t_1=2,249\) og \(t_2=2\pi-t_1=4,034\) og

\(\overrightarrow{r(t_1)}= \overrightarrow{r(t_2)}=(x(t_1), y(t_1))=(x(t_2), y(t_2))=(-2,51, 0,85)\)