Omskrivning fra parameterfremstilling til sædvanlig funktion

For visse vektorfunktioner er det muligt at omskrive parameterfremstillingen \((x(t),y(t))\) til en sædvanlig funktion af typen \(y=f(x)\).

Et tilfælde er allerede vist i eksempel 1 i afsnit 2.2, hvor vi omskrev parameterfremstillingen for en ret linje, nemlig \((x(t),y(t))=(t+2, 2\cdot t+8)\), hvor \(-\infty<t<+\infty\),  til funktionen \(y=2\cdot x+4\), hvor \(-\infty<x<+\infty\).

Når vi skal foretage omskrivning af en parameterfremstilling, skal vi først sikre os, at funktionen bliver éntydig. Det vil sige, at der for enhver x-værdi kun er én y-værdi. Det kan ofte kræve, at funktionen opdeles i to eller flere del-funktioner, som vist i eksemplerne nedenfor.

I nogle tilfælde er det ikke muligt (eller ikke anbefalelses­værdigt at forsøge!) at omskrive parameterfremstillingen. Det gælder f.eks. den snoede kurve i afsnit 4 og Archimedes spiral i afsnit 5.

Eksempel 1

Cirklen er som parameterfremstilling givet ved, se figur 16:

\((x(t),y(t))=(r\cdot \cos(\omega t), r\cdot \sin(\omega t))\), \(0\leq t\leq \frac{2\pi}{\omega}\)

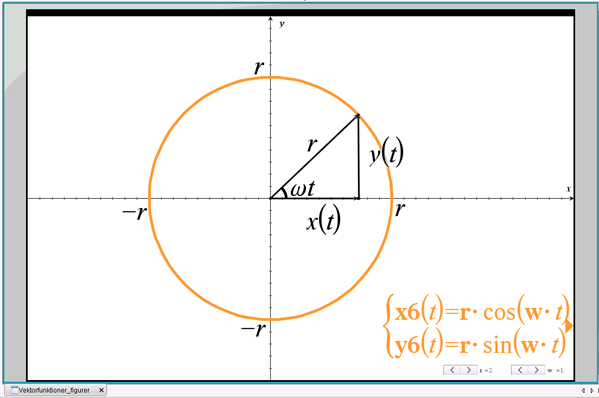
Figur 16    Cirklen

Umiddelbart har cirklen to y-værdier for hver x-værdi (i intervallet \(-r<x<r\)), men hvis vi opdeler cirklen i to halvcirkler, hhv. over og under x-aksen, opnår vi den ønskede éntydighed.

For ethvert punkt på cirklen gælder: \(x(t)^2+y(t)^2=r^2\), som ved omskrivning giver: \(y(t)^2=r^2-x(t)^2\). Denne ligning har to løsninger:

halvcirklen over x-aksen:              \(y_1(x)=\sqrt{r^2-x^2}=r\cdot\sqrt{1-(\dfrac{x}{r})^2}\)  
halvcirklen under x-aksen:        \(y_2(x)=-\sqrt{r^2-x^2}=-r\cdot\sqrt{1-(\dfrac{x}{r})^2}\)

For begge funktioner er definitionsmængden: \(-r\leq x\leq r\).

Eksempel 2

På helt tilsvarende måde kan en ellipse, se figur 17:

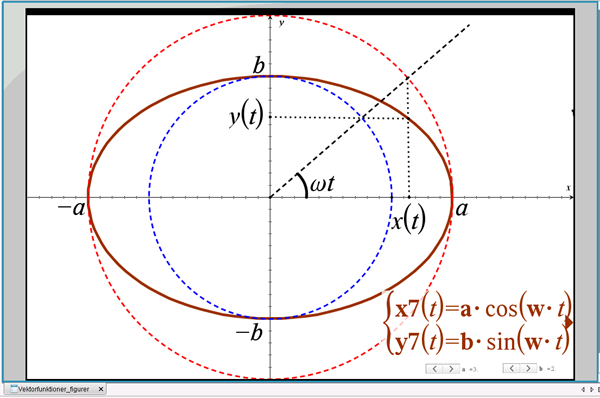
Figur 17    Ellipsen

med parameterfremstillingen: \((x(t),y(t))=(a\cdot \cos(\omega t), b\cdot \sin(\omega t))\), \(0\leq t\leq \frac{2\pi}{\omega}\), opdeles i to halv-ellipser, hhv. over og under x-aksen.

Vi udnytter, at der for ellipsen gælder: \((\dfrac{x(t)}{a})^2+(\dfrac{y(t)}{b})^2=1\), og omskrivningen til to del-funktioner er:

halv-ellipsen over x-aksen:            \(y_1(x)=b\cdot\sqrt{1-(\dfrac{x}{a})^2}\)

halv-ellipsen under x-aksen:     \(y_2(x)=-b\cdot\sqrt{1-(\dfrac{x}{a})^2}\)

For begge funktioner er definitionsmængden: \(-a\leq x\leq a\).

Eksempel 3

Den liggende parabel fra afsnit 1 er givet ved parameter­fremstillingen: \((x(t),y(t))=(2t^2+4t-16,t)\), hvor \(-\infty< t<+\infty\), se figur 18.

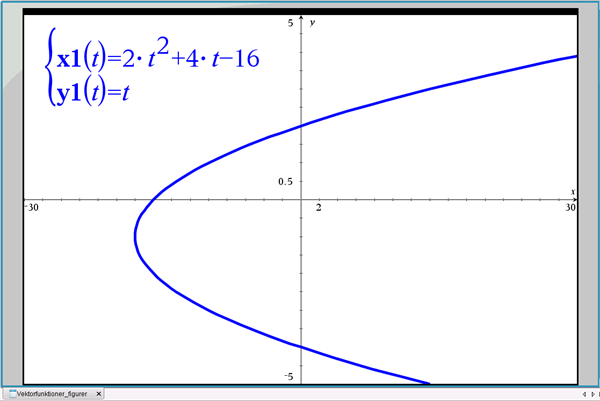
Figur 18    Liggende parabel

Vi kan opdele parablen i to halvdele, som vi kalder parabel-grene. De to parabelgrene ligger hhv. over og under den vandrette symmetriakse \(y=-1\), der går gennem parablens toppunkt \((x_T,y_T)=(-18,-1)\). 

For en vilkårlig x-værdi, hvor \(-18\leq x<+\infty\), kan vi bestemme de tilhørende y-værdier på de to parabel-grene som løsningerne til ligningen \(2t^2+4t-16=x\), idet vi fra parameterfremstillingen har, at \(y=t\).

Ligningen omskrives nemt til den velkendte form for en andengradsligning: \(2y^2+4y-(x+16)=0\), som har to løsninger (idet diskriminanten er \(d=b^2-4ac=16+8\cdot (x+16)=16\cdot (\dfrac{x}{2}+9)\)):

øverste parabel-gren:  \(y_1(x)=\dfrac{-b+\sqrt{d}}{2a}=\dfrac{-4+4\cdot\sqrt{\dfrac{x}{2}+9}}{4}=-1+\sqrt{\dfrac{x}{2}+9}\) 

nederste parabel-gren:  \(y_1(x)=\dfrac{-b-\sqrt{d}}{2a}=\dfrac{-4-4\cdot\sqrt{\dfrac{x}{2}+9}}{4}=-1-\sqrt{\dfrac{x}{2}+9}\)

For begge funktioner er definitionsmængden:\(-18\leq x<+\infty\).