Vektorer i 3D

Præcis som i 2D er en 3D-vektor en pil med en retning og en længde.

I 3D har en vektor tre koordinater, der svarer til vektorens længde (regnet med fortegn) i hver af de tre aksers retninger. Første koordinaten svarer altså til, hvor langt man går langs x-aksen, andenkoordinaten hvor langt man går langs y-aksen, og tredjekoordinaten langs z-aksen.

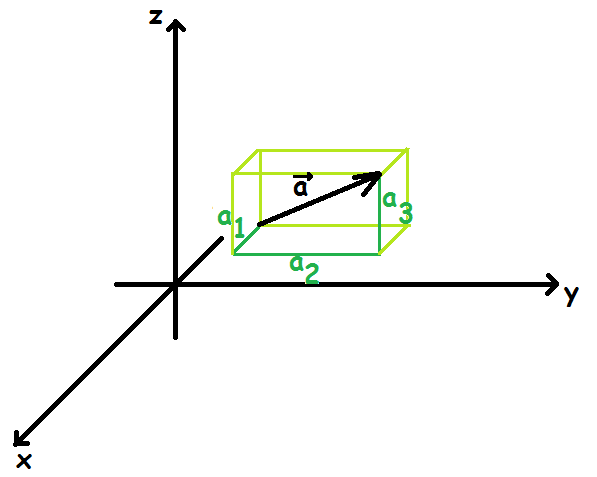
$$\overrightarrow{a}=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix}$$

De fleste begreber om vektorer fra 2D kan overføres direkte til 3D. Imidlertid gælder det ikke for tværvektor-begrebet. I rummet kan man nemlig ikke tale om at rotere en vektor 90º mod uret, da "mod uret" afhænger af, hvor man ser fra. Der vil således være uendeligt mange måder at konstruere en vektor på, der står vinkelret på en bestemt vektor. Herunder er tegnet to vektorer, b og c, der begge står vinkelret på vektor a (men som ikke er vinkelrette på hinanden)

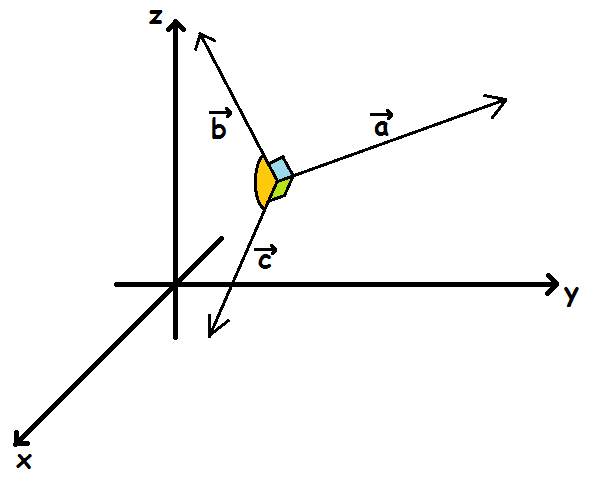
Udover tværvektorbegrebet, overfører vi heller ikke determinanten til 3D. Dette skyldes, at determinanten er defineret ud fra tværvektorer. Men ellers overføres alle de andre begreber. Nulvektoren i 3D er således

$$\overrightarrow{0}=\begin{pmatrix}0\\0\\0\end{pmatrix}$$

En stedvektor har samme koordinater, som det punkt, den fører hen til. Man kan konstruere en vektor mellem to punkter ved at trække deres koordinater fra hinanden

$$\overrightarrow{AB}=\begin{pmatrix}b_1-a_1\\b_2-a_2\\b_3-a_3\end{pmatrix}$$