Projektion af punkt på plan

Hvis man har et punkt og et plan, kan man ønske at projicere punktet ned på planen. Projektionen svarer til det punkt i planen, man rammer, hvis man bevæger sig vinkelret fra punktet ind mod planen.

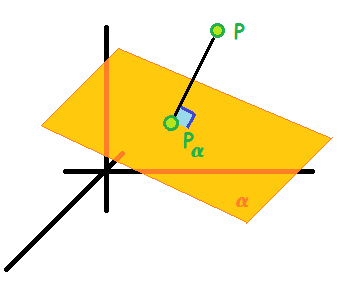
Hvordan finder man projektionen

Når man ønsker at finde koordinatsættet for projektionen af et punkt på et plan, gør man det i flere trin.

Først konstruerer man en linje, der står vinkelret på planen og som går gennem punktet.

Dernæst finder man skæringspunktet mellem planen og linjen. Skæringspunktet er projektionen.

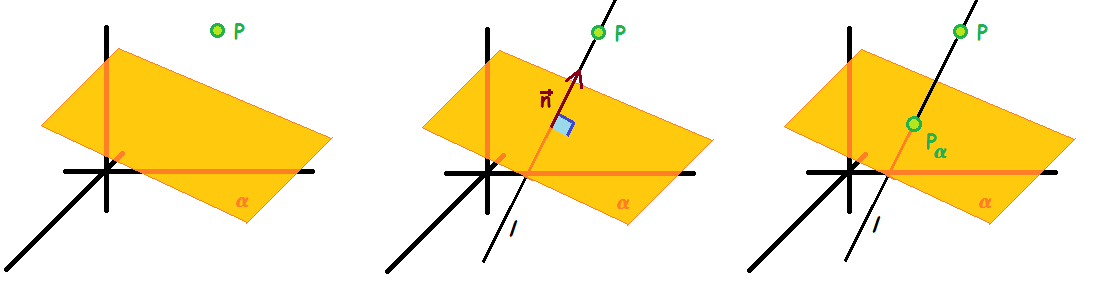
Det er let at konstruere en linje gennem punktet som står vinkelret på planen. Man bruger planens normalvektor som retningsvektor for linjen (så sikrer man sig at linjen er vinkelret på planen) og man bruger punktet som det faste punkt på linjen.

Skæringspunktet mellem linjen og planen finder man på den måde, der er beskrevet i afsnittet om skæringer mellem linjer og planer.

Lad os se på et eksempel.

$$\alpha:\:3x-y+4z+26=0\\P(1,2,3)$$

Vi ønsker at projicere P ind på α.

Vi aflæser koordinaterne for planens normalvektor ud fra dens ligning

$$\overrightarrow{n}=\begin{pmatrix}3\\-1\\4\end{pmatrix}$$

Denne bruger vi som retningsvektor for linjen, l, gennem P og vinkelret på α.

Vi kan altså skrive linjens parameterfremstilling op således:

$$l:\:\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+t\cdot\begin{pmatrix}3\\-1\\4\end{pmatrix}$$

Man kan også skrive parameterfremstillingen op som de tre koordinatfunktioner

$$x=1+3t$$

$$y=2-t$$

$$z=3+4t$$

Nu skal vi finde skæringspunktet mellem linjen og planen. Det gør vi ved at sætte koordinatfunktionerne ind i planens ligning

$$\\3({\color{Red} {1+3t}})-({\color{Red} {2-t}})+4({\color{Red} {3+4t}})+26=0$$

$$3+9t-2+t+12+16t+26=0$$

$$26t+39=0$$

$$t=\frac{-39}{26}=-1,5$$

Nu har vi fundet ud af, at skæringspunktet findes, når t= -1,5.

Vi indsætter denne t-værdi i linjens parameterfremstilling for at se, hvilket punkt, det svarer til.

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}+({\color{Red} {-1,5}})\cdot\begin{pmatrix}3\\-1\\4\end{pmatrix}=$$

$$=\begin{pmatrix}1-1,5\cdot3\\2-1,5\cdot(-1)\\3-1,5\cdot4\end{pmatrix}=\begin{pmatrix}1-4,5\\2+1,5\\3-6\end{pmatrix}=\begin{pmatrix}-3,5\\3,5\\-3\end{pmatrix}$$

Altså er projektionen af punktet på planen

$$P_\alpha=(-3.5,\:3.5,\:-3)$$