Omdrejningslegemer

Et omdrejningslegeme (eller et rotationslegeme) er den tredimensionale figur, man får, hvis man roterer en funktion 360 grader rundt om x-aksen. Det er vigtigt, at funktionen er kontinuert, og at den kun har positive værdier.

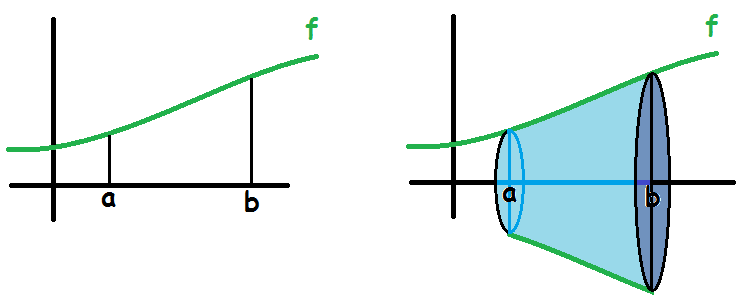
Man kan beregne volumen af omdrejningslegemet ved hjælp af følgende formel

$$V=\pi\cdot\int_a^b(f(x))^2\:dx$$

Lad os regne nogle eksempler.

Vi ønsker at beregne volumen af keglen med højde 10 og radius 5. 

Vi indtegner siden af keglen i et koordinatsystem som vist nedenfor

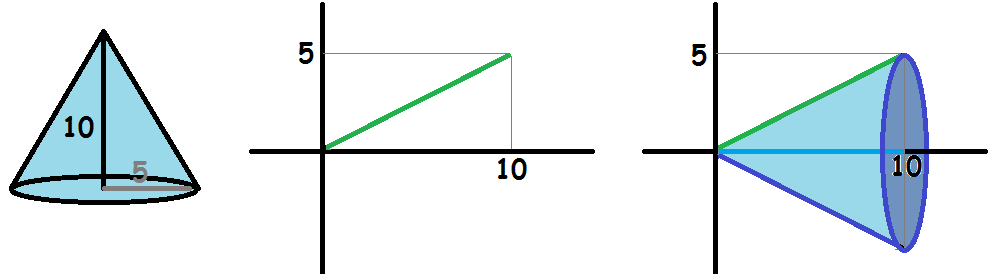
Vi har to punkter på grafen, (0, 0) og (10,5), så vi kan bestemme den lineære funktions forskrift

$$a=\frac{y_2-y_1}{x_2-x_1}=\frac{5-0}{10-0}=\frac{5}{10}=\frac{1}{2}$$

og, da vi har lagt funktionen, så den skærer akserne i (0, 0), så er b=0.

Altså er

$$f(x)=\frac{1}{2}x$$

Vi er interesserede i intervallet [0;10].
Nu sætter vi ind i formlen for volumen af omdrejningslegeme:

$$V=\pi\int_0^{10}(\frac{1}{2}x)^2\:dx=\pi\int_0^{10}\frac{1}{4}x^2\:dx \\=\pi\left[\frac{1}{4}\cdot\frac{1}{3}x^3 \right ]_0^{10} \\ =\pi\cdot\left(\frac{1}{12}\cdot1000-\frac{1}{2}\cdot0 \right )=\frac{1000\pi}{12}\approx261,8$$

Vi tager et andet eksempel.

Vi vil rotere andengradspolynomiet

$$f(x)=-5x^2+5x=-5x(x-1)$$

om x-aksen mellem dets to rødder 0 og 1.

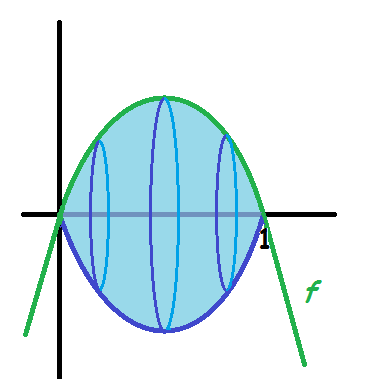
Mellem de to rødder er polynomiet positivt, så derfor må vi benytte vores formel.

$$V=\pi\int_0^1(-5x(x-1))^2\:dx$$

Først regner vi lidt på integranden (indmaden i integralet) ved hjælp af potensregler og
kvadratsætninger.

$$(-5x(x-1))^2=(-5x)^2(x-1)^2 \\ =25x^2(x^2+1-2x)=25x^4+25x^2-50x^3$$

Nu er vi klar til at udregne integralet.

$$V=\pi\int_0^125x^4+25x^2-50x^3\:dx \\ =\pi\left[\frac{25}{5}x^5+\frac{25}{3}x^3-\frac{50}{4}x^4 \right ]_0^1 \\ =\pi\left(5\cdot1^5+\frac{25}{3}\cdot1^3-\frac{50}{4}\cdot1^4-0 \right ) \\ =\pi\left(\frac{5\cdot12}{12}+\frac{25\cdot4}{12}-\frac{50\cdot3}{12} \right ) \\ =\pi\left(\frac{60+100-150}{12} \right )=\frac{10\pi}{12} =\frac{5\pi}{6}\approx2,618$$

---

Videolektion