Parameterfremstillingen for den rette linje

Den rette linje i et koordinatsystem er du vant til at se beskrevet ved forskriften \(y(x)=a\cdot x+b\), hvor a angiver linjens hældningskoefficient (stig­ningstal) og b angiver linjens skæring med y-aksen.

At a er linjens hældningskoefficient, betyder, at vektoren \(\overrightarrow{r}=(1,a)\) er en retningsvektor for linjen, se figur 4.

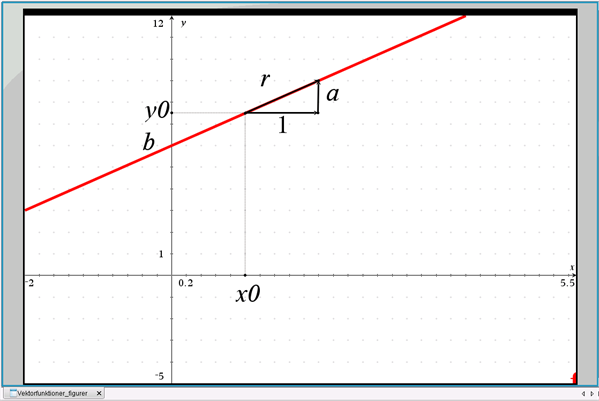
Figur 4      Afbildning af en ret linje

Linjen kan også beskrives ved en parameterfremstilling med udgangspunkt i retningsvektoren og et vilkårligt punkt på linjen \((x_0,y_0)\). På figur 4 kan du se, at man kan få alle andre punkter på linjen ved at addere retnings­vektoren \(\overrightarrow{r}=(1,a)\) multipliceret med et vilkårligt tal til punktet \((x_0,y_0)\):

\(\overrightarrow{r(t)}=(x(t),y(t))=(x_0,y_0)+t\cdot \overrightarrow{r}=(t+x_0, a\cdot t+y_0)\),
hvor \(-\infty < t < +\infty\).

Hvis vi vælger linjens skæringspunkt med y-aksen som udgangspunkt for parameter­frem­stillingen, er \((x_0,y_0)=(0,b)\), og så bliver parameter­frem­stillingen:

\(\overrightarrow{r(t)}=(x(t),y(t))=(t, a\cdot t+b)\), hvor \(-\infty < t < +\infty\).

Eksempel 1

Bestem hældningen og skæring med y-aksen – og dermed forskriften – for en linje givet ved parameterfremstillingen:

\(\overrightarrow{r(t)}=(x(t),y(t))=(t+2, 2\cdot t+8)\), hvor \(-\infty < t < +\infty\).

Skæring med y-aksen:

\(x(t_0)=0\implies t_0=-2\) og dermed \(y(t_0)=2\cdot t_0+8=4\).

Hældningen er forholdet mellem faktorerne til \(t\) i hhv. \(y(t)\) og \(x(t)\):

\(a=\dfrac{2\cdot t}{t}=2\) og dermed er \(y(x)=2x+4\).

Eksempel 2

Find skæringspunktet mellem de to linjer givet ved:

\(\overrightarrow{r(t)}=(x(t),y(t))=(t+2, 2\cdot t+8)\), hvor \(-\infty < t < +\infty\)

\(\overrightarrow{r(s)}=(x(s),y(s))=(s, 3\cdot s-6)\),      hvor \(-\infty < s < +\infty\).

I linjernes skæringspunkt er \(x(s)=x(t)\) og \(y(s)=y(t)\):

\(x(s)=x(t)\implies s=t+2\), som indsættes i ligningen for y:

\(y(s)=y(t)\implies 3(t+2)-6=2t+8\implies 3t=2t+8\)

og dermed \(t=8\) og \(s=t+2=10\).

Ved at indsætte værdierne af s og t i de to parameterfrem­stillinger finder vi linjernes skæringspunkt \((x,y)=(10,24)\), hvilket også ses i figur 5.

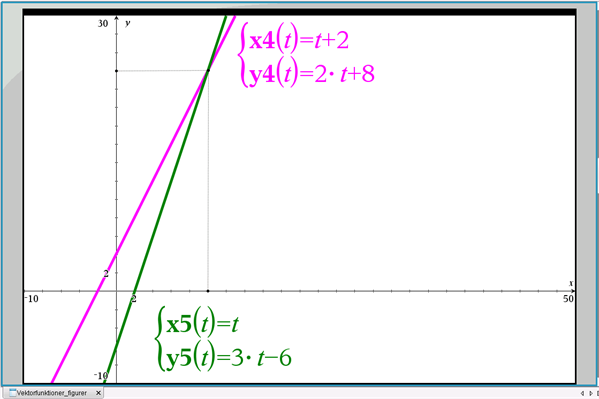
Figur 5      Skæringspunkt mellem to linjer