Ubestemt integral
Før vi går i gang med at definere bestemte og ubestemte integraler vil vi gennemgå lidt notation og terminologi.
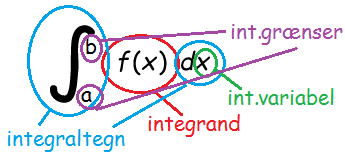
For at vide, at man skal integrere en funktion, markerer man det med et integraltegn. Et integraltegn består af to dele. Til venstre skriver man et "langt s" og til højre skriver man et "d" efterfulgt af den variabel, man integrerer med hensyn til (oftest bare \(\mathrm{d}x\)). S'et såvel som \(\mathrm{d}x\) er bare rene symboler.
Imellem dem står den funktion, man ønsker at integrere. Denne kaldes integranden, men omtales tit som "indmaden". De bestemte integraler har derudover en øvre og en nedre integrationsgrænse, som man skriver ved hhv. top og bund af det lange s.
Ubestemt integral
I forrige afsnit definerede vi, hvad en stamfunktion er. At finde det ubestemte integral til en funktion \(f\) er simpelthen bare at bestemme en stamfunktion til \(f\). Skrevet matematisk:
$$\int f(x)\,\mathrm{d}x=F(x)$$
Dette læses som "det ubestemte integral af \(f\) (mht. \(x\)) er lig med en stamfunktion til \(f\)".
Man skal huske at tilføje en konstant til den stamfunktion, man finder. På den måde har man nemlig skrevet alle stamfunktionerne op på én gang.
Lad os finde nogle ubestemte integraler.
Hvis
$$f(x)=x$$
så er
$$F(x)=\int x\,\mathrm{d}x=\frac{1}{2}x^2+k \ .$$
Vi tjekker om det er rigtigt vha. integrationsprøven
$$F'(x)=\left(\frac{1}{2}x^2+k\right)'=\frac{1}{2}\cdot2x^{2-1}+0=\frac{2}{2}x=x=f(x) \ .$$
Hvis vi i stedet har
$$f(x)=x^4+\frac{1}{x},\qquad x>0$$
så er
$$F(x)=\int x^4+\frac{1}{x}\,\mathrm{d}x=\frac{1}{5}x^5+\ln(x)+k,\qquad x>0 \ .$$
Igen tjekker vi efter med integrationsprøven
$$F'(x)=\left(\frac{1}{5}x^5+\ln(x)+k\right)'=\frac{1}{5}\cdot5x^{5-1}+\frac{1}{x}+0=x^4+\frac{1}{x}=f(x)$$
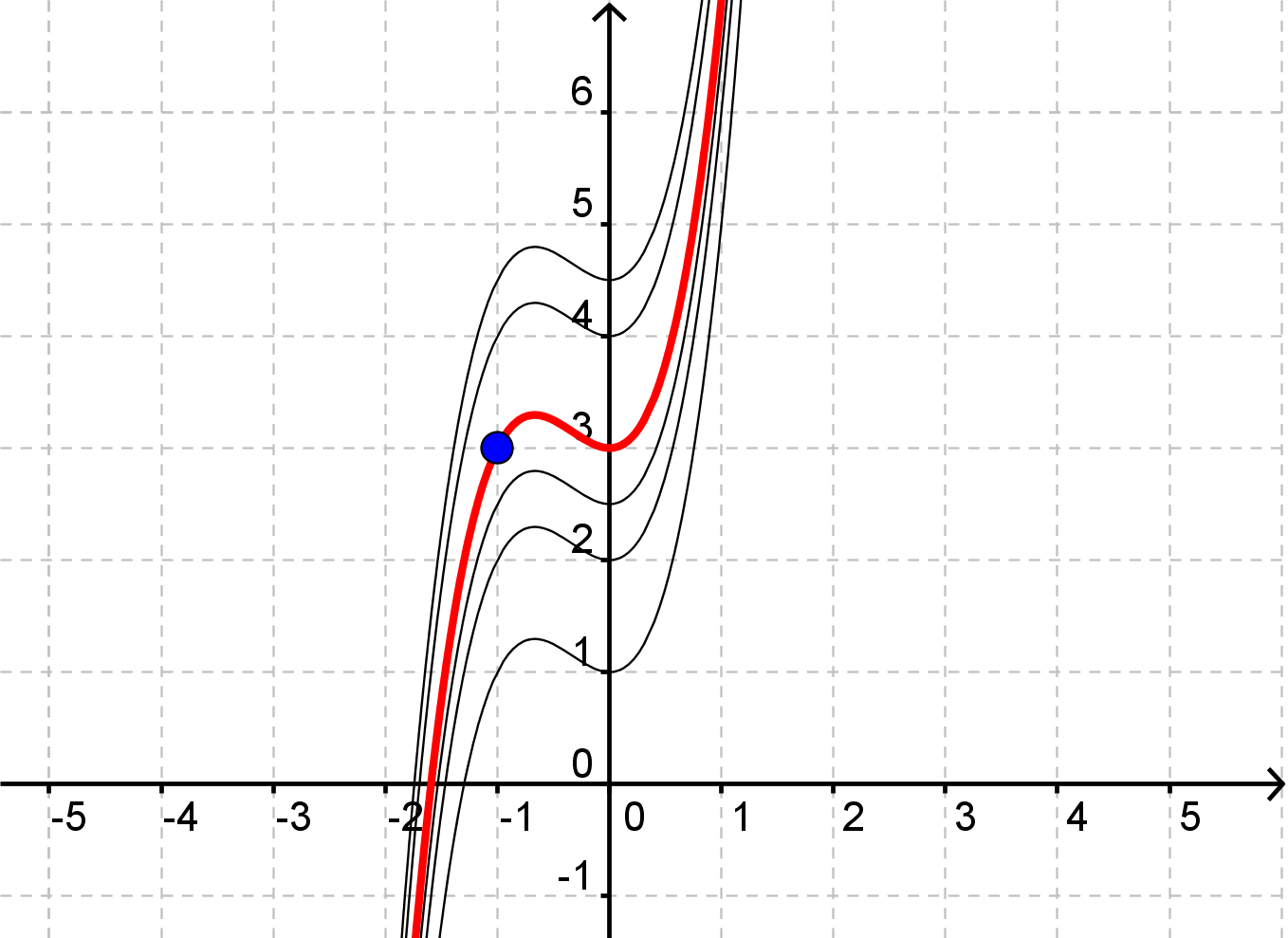
Bestem en stamfunktion gennem et punkt
Ovenfor har vi brugt det ubestemte integral til at finde alle stamfunktioner til en funktion. I visse tilfælde kan det være nyttigt at finde en bestemt stamfunktion.
En opgave kunne f.eks. lyde:
$$f(x)=6x^2+4x$$
Find den stamfunktion til \(f\), der går igennem punktet (-1, 3).
Først finder vi alle stamfunktionerne, og bagefter bestemmer vi \(k\) ud fra vores startbetingelse.
$$F(x)=\int 6x^2+4x\,\mathrm{d}x=2x^3+2x^2+k$$
(Du kan selv tjekke efter med integrationsprøven, at dette er rigtigt).
Nu ønsker vi at finde ud af hvilken af disse stamfunktioner, der går gennem (-1, 3).
Vi sætter -1 ind på \(x\)'s plads og 3 på stamfunktionsværdiens plads.
$$
\begin{align}
F(-1) & = 3 \\
2\cdot(-1)^3+2\cdot(-1)^2+k & = 3 \\
-2+2+k & = 3 \\
k & = 3
\end{align}
$$
Den stamfunktion vi leder efter har altså \(k=3\). Derfor er svaret på opgaven
$$F(x)=2x^3+2x^2+3$$
Nedenfor er indtegnet forskellige stamfunktioner til \(f\).
Kun én af dem går igennem (-1, 3).