Introduktion til Multipel regression
Introduktion
Fra simpel lineær regressions analyse ved vi, hvordan man med mindste kvadraters metoden bestemmer den lineære funktion, som bedst passer til en række observationer i 2D planen.
Vi har altså her observationer \((y_i, x_i)\) for \(i=1,\ldots,n\) og ønsker at bestemme konstanterne \(a\) og \(b\) på en sådan måde, at den lineære funktion
\(
y = a + b x
\)
ligger så tæt på alle observationer \((y_i, x_i)\) som muligt.
Verden er dog sjældent så simpelt indrettet, at man kan beskrive en afhængig variabel \(y\) med kun en enkelt forklarende variabel \(x\).
Multipel regression er en udvidelse af simpel regression, hvor vi i stedet for en enkelt forklarende variabel har to eller flere forklarende variable. Forklarende variable kaldes til tider også for kovarianter mens afhængige variable somme tider omtales som respons variable.
Model
Vi har \(n\) observationer \(y_i,x_{i1},x_{i2},\ldots,x_{ip}\) hvor \(i=1,\ldots,n\) og ønsker at bestemme konstanter \(b_0,b_1,b_2,\ldots,b_p\), så funktionen
\(y = b_0 + b_1 x_1 + b_2 x_2 + \cdots b_p x_p
\)
ligger så tæt på alle punkterne \(y_i,x_{i1},x_{i2},\ldots,x_{ip}\) som muligt. Konstanterne kaldes for regressionskoefficienterne.
Bemærk, at der nu er et dobbelt indeks på \(x\)'erne. Det er nødvendigt, da vi nu har \(p\) forklarende variable i stedet for blot en enkelt forklarende variabel. Så når vi skriver
\(
x_{ij}, \quad i=1,\ldots,n \quad \textrm{ og } \quad j=1,\ldots,p
\)
er der tale om den \(j\)'te forklarende variable for den \(i\)'te observation.
Vi kan stille observationerne op i en tabel
| Observation | Afhængig variabel | Forklarende variable |
| \(Y\) | \(X_1\) \(X_2\) \(\cdots\) \(X_p\) | |
| 1 | \(y_1\) | \(x_{11}\) \(x_{12}\) \(\cdots\) \(x_{1p}\) |
| 2 | \(y_2\) | \(x_{21}\) \(x_{22}\) \(\cdots\) \(x_{2p}\) |
| 3 | \(y_3\) | \(x_{31}\) \(x_{32}\) \(\cdots\) \(x_{3p}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) \(\vdots\) \(\cdots\) \(\vdots\) |
| n | \(y_n\) | \(x_{n1}\) \(x_{n2}\) \(\cdots\) \(x_{np}\) |
for på den måde at vise, at vi har \(p\) forklarende variable og \(n\) observationer.
Regressionskoefficienter bliver normalt fundet (estimeret) ved brug af mindste kvadrater metoden, hvor man vælger \(b_0, b_1, \ldots , b_p\) således at udtrykket
\begin{equation}\label{eq:sse}
SSE =\sum^n_{i=1} {\big(y_i - b_0 - b_1 x_{i1} - b_2 x_{i2} - \cdots - b_p x_{ip} \big)}^2
\end{equation}
minimeres. SSE er engelsk for Sum of Squares Errors. Dette er samme fremgangsmetode som kendes fra simpel lineær regression. \(b_0\) kaldes for skæringen og de øvrige \(b\)'er kaldes hældninger.
Formlen for koefficienterne \(b_0,b_1,b_2,\ldots,b_p\) er noget mere kompliceret i det generelle tilfælde, så den springer vi over her. Men nedenfor gennemgår vi et eksempel på, hvordan man kan bestemme koefficienter ved brug af Microsoft Excel.
Residualer
Når vi har bestemt regressionskoefficienterne \(b_0,b_1,b_2,\ldots,b_p\) så kan vi udregnede de fittede værdier for observationerne \(x_{i1},x_{i2},\ldots,x_{ip}\) hvor \(i=1,\ldots,n\). For den \(i\)'te observation er den fittede værdi
\(
\widehat{y_i} = b_0 + b_1 x_{i1} + b_2 x_{i2} + \cdots b_p x_{ip}
\)
og vi definerer residualer som værende forskellen \(e_i\) mellem observationen \(y_i\) og den fittede værdi \(\widehat{y_i}\)
\(
e_i = y_i - \widehat{y_i}
\)
Bemærk at den før omtalte ligning for SSE også kan skrives
\(
SSE =\sum^n_{i=1} {\big(y_i - b_0 - b_1 x_{i1} - b_2 x_{i2} - \cdots - b_p x_{ip} \big)}^2 = \sum^n_{i=1} {\big(y_i - \widehat{y_i} \big)}^2 = \sum^n_{i=1} {e_i}^2
\)
så når vi finder minimum for \(SSE\), så minimerer vi residualerne eller med andre ord - forskellen mellem de observerede og fittede værdier.
Visualisering af løsningen
I tilfældet med simpel regression bestemmer vi en ret linje som passer bedst til observationerne. Det er umuligt at visualisere multipel regression i det generelle tilfælde. For det særlige tilfælde, hvor vi har to forklarende variable \(x_1\) og \(x_2\) og dermed modellen
\(
y = b_0 + b_1 x_1 + b_2 x_2
\)
så kan vi stadig visualisere løsningen. Vi kan tænke på observationerne \((x_{i1}, x_{i2}, y_i), i=1,\ldots,n\) som punkter i rummet i 3D koordinatsystemet med akserne \(X_1, X_2\) og \(Y\).
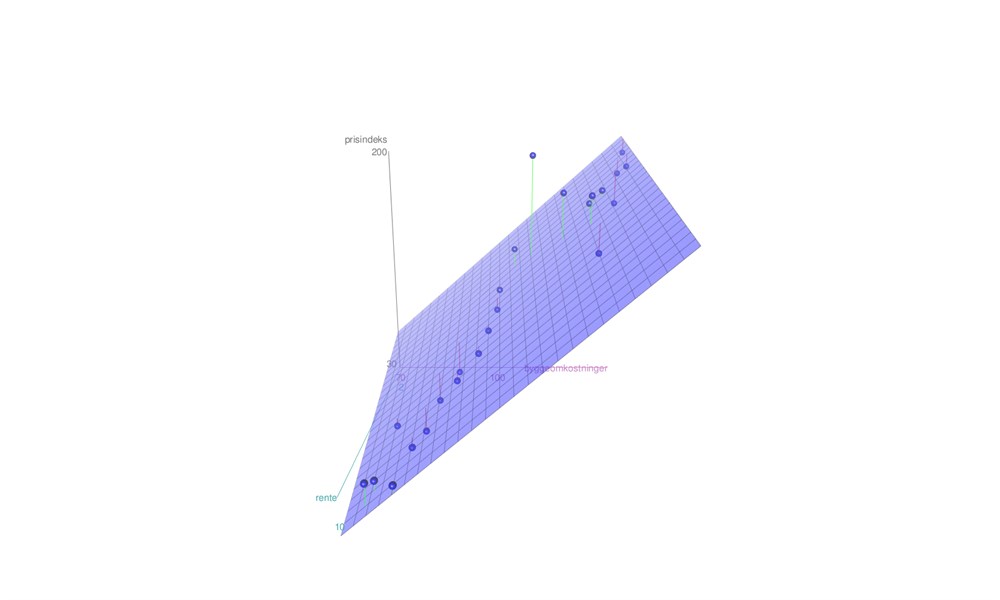
Løsningen er nu ikke længere en ret linje, men derimod den plan som ligger tættest på alle punkterne. På figuren kan vi også se residualerne - de er plottet som linjer mellem observationerne og planen. Nogle observationer ligger over planen og er markeret med en grøn linje, mens andre observationer ligger under planen og er markeret med en rød linje.
Det kan være svært ud fra en enkel vinkel at forestille sig, hvordan løsningen ud. Prøv at se på følgende optagelse, hvor vi kan se planen fra en række forskellige vinkler.
Eksempel
Lad os se på et (simplificeret) eksempel på multipel regressionsanalyse. Eksemplet er hentet fra opgaven Prisdannelse på ejerlejligheder i København af Vibeke Stål og Anne Melvej Stennevad. Forfatterne undersøger, om der er en lineær sammenhæng mellem prisen på ejerlejligheder i København og en række faktorer såsom fx rente og byggeomkostninger.
\(\label{eq:model}
\textrm{prisindeks} = b_0 + b_1 * \textrm{byggeomkostninger} + b_2 * \textrm{rente}
\)
Hvordan bestemmer man regressionskoefficienterne \(b_0, b_1\) og \(b_2\), hvis vi har observationer som vist her i Excel
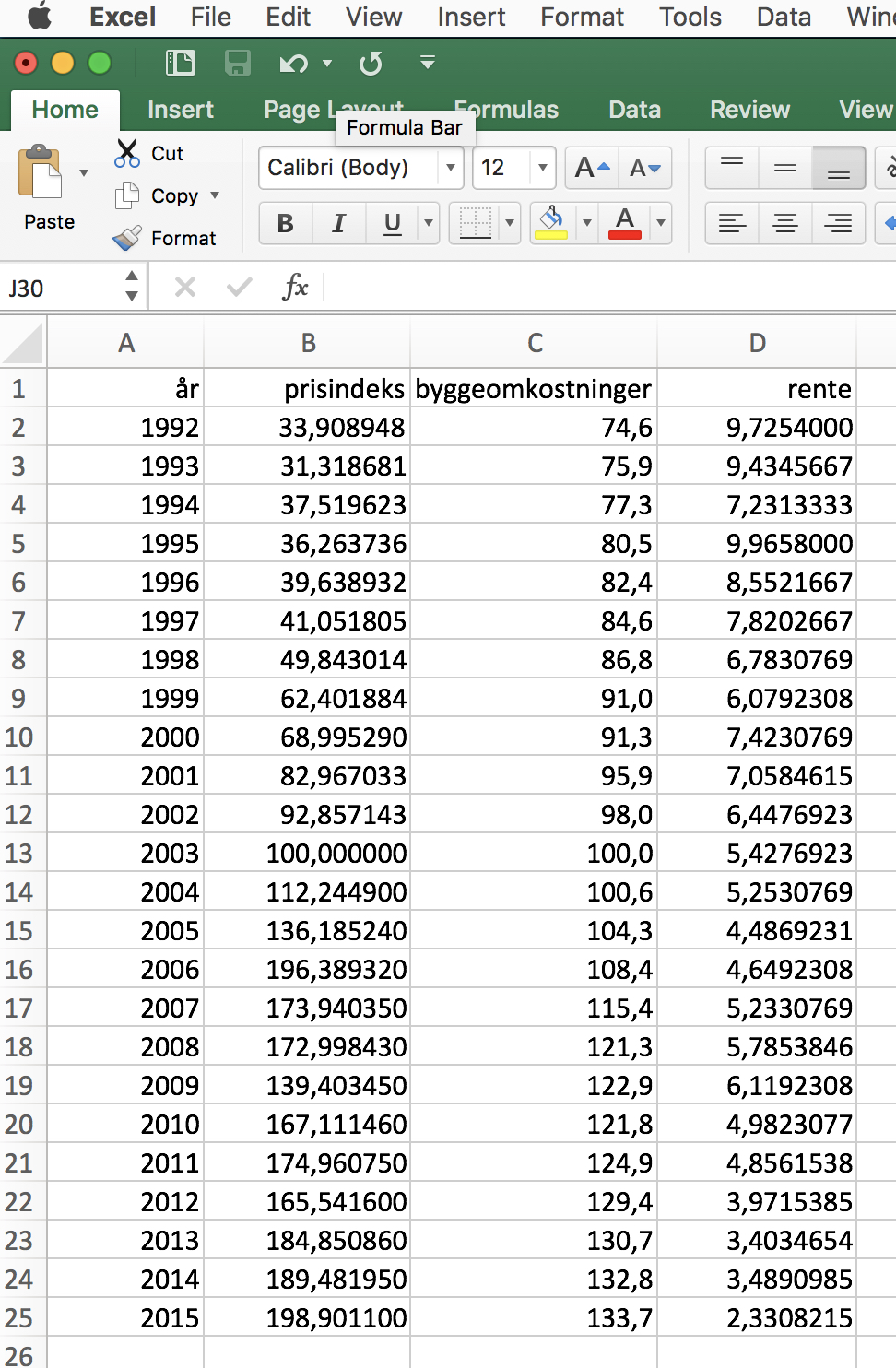
Hvis du selv ønsker at arbejde med dette datasæt, så kan det downloades via dette link.
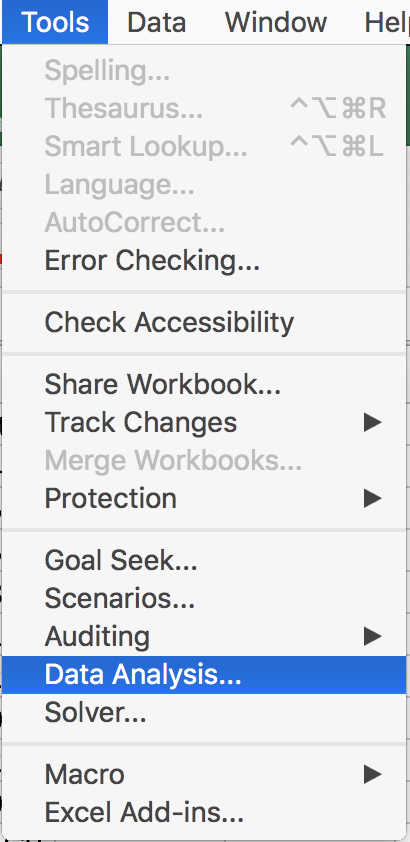
I menuen under "Tools'' finder man "Data Analysis''. Hvis Data Analysis ikke er en del af menuen, så er her en vejledning til hvordan man får den installeret i Excel.
og dernæst fås en oversigt over de forskellige analyseværktøjer. Vælg "Regression''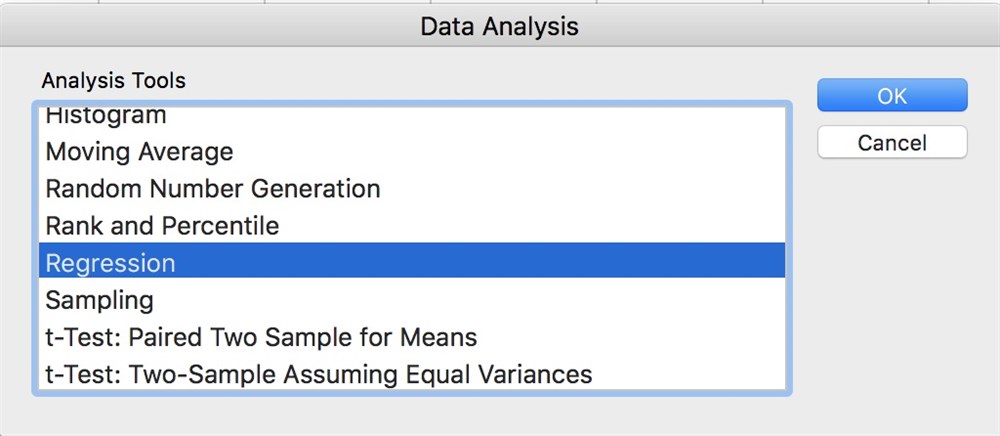
Så dukker denne regression menu op
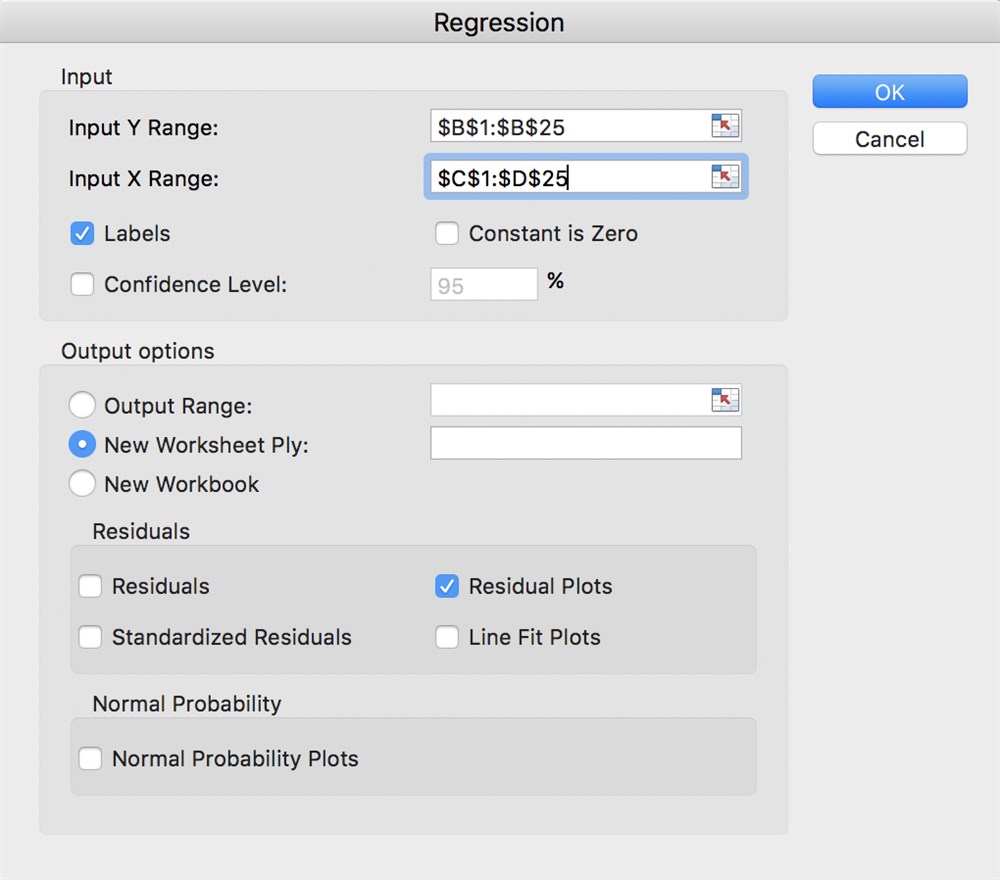
Her har vi som "Input Y Range'' valgt kolonnen med prisindeks (inkl. overskriften). Dette er vores afhængige variable. Dernæst har vi som "Input X Range'' valgt kolonnerne med data for byggeomkostninger og renter (igen inkl. overskrift). Ved at sætte kryds i "Labels'' checkboksen fortæller vi Excel, at vores valg af inputdata indeholder overskrifter. Det gør det nemmere at læse resultaterne. Som det sidste vælger vi også "Residual Plots''.
Som udgangspunkt bliver alle resultater placeret i en nyt Excel sheet. Så er det lettere at slette dette sheet og begynde forfra, hvis man får behov for det.
Der er en masse output fra beregningen, men i første omgang fokuseres vi på regressionskoefficienterne
Indsætter vi de fundne koefficienter i vores model får vi regressionsligningen
\(
\textrm{prisindeks} = -90,95 + 2,35 * \textrm{byggeomkostninger} - 6,67 * \textrm{rente}
\)
Efter at have bestemt selve modellen kigger vi på tallene under overskriften "Regression Statistics'':
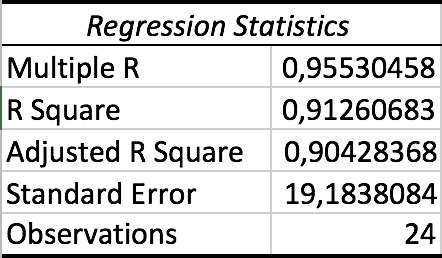
Her sætter vi fokus på Multiple R og R Square. På dansk kaldes disse to værdier for korrelations- og determinationskoefficienten.
