Skæring med koordinatsystemets akser
På koordinatsystemets y-akse er \(x=0\), og på koordinatsystemets x-akse er \(y=0\).
For at undersøge om en vektorfunktion med en given parameterfremstilling indeholder skæringspunkter med koordinatsystemets akser, skal vi derfor finde eventuelle løsninger til de to ligninger:
Skæring med y-aksen: \(x(t)=0\)
Skæring med x-aksen: \(y(t)=0\)
Eksempel:
Vi vender tilbage til den liggende parabel fra afsnit 1, se figur 9. Her er: \(x(t)=2t^2+4t-16\) og \(y(t)=t\), hvor \(-\infty < t < +\infty\).
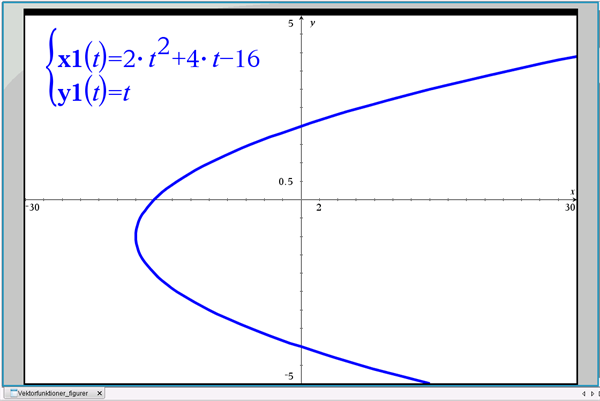
Figur 9 Liggende parabel
Skæring med y-aksen:
\(x(t)=2t^2+4t-16=0\) med løsningerne \(t=-4\) og \(t=2\), hvor \(y(-4)=-4\) og \(y(2)=2\), og dermed er skæringspunkterne \((x,y)=(0,-4)\) og \((0,2)\).
Skæring med x-aksen:
\(y(t)=t=0\) med løsningen \(t=0\), hvor \(x(0)=-16\), og dermed er skæringspunktet \((x,y)=(-16,0)\).
