Introduktion til parameterfremstillinger

Vektorfunktioner går ud på at beskrive kurver i et koordinat­system ved hjælp af en parameterfremstilling.

Vi bruger betegnelsen kurver ifm. parameter­fremstil­linger, så der ikke sker forveksling med grafer, der hører til sædvan­lige funk­tioner.

Tidligere har vi opfattet \(x\) som den uafhæn­gige variabel og \(y\) som den afhængige variabel. Nu indfører vi en ny uafhængig variabel, \(t\). Hermed bliver både \(x\) og \(y\) afhængig af \(t\), og vi skriver hhv. x(t) og y(t).

Ofte vil vi benytte parameterfremstillingen til at beskrive banekurven for en bevægelse, hvor \(t\) angiver tiden, og hvor \(x(t)\) og \(y(t)\) angiver positionen, dvs. hhv. x- og y-koordinaten for bevægelsen til tiden \(t\).

Et vilkårligt punkt på kurven kan beskrives ved punktets stedvektor i et sædvanligt koordinatsystem, se figur:

\(\overrightarrow{r(t)}=(x(t),y(t))\)

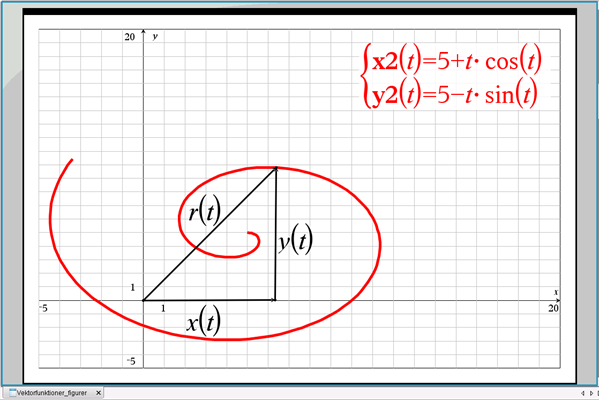
Figur 3      Afbildning af en vektorfunktion. \(\overrightarrow{r(t)}\) er stedvektor til punkter på kurven

Vi kalder \(\overrightarrow{r(t)}\) for en vektorfunktion, og for enhver værdi af t kan vi beregne de tilhørende værdier x(t) og y(t) og plotte punktet i koordinatsystemet. Når vi gør dette for alle værdier af t i definitions­mængden, fremkommer kurven.

Ved at bruge en parameterfremstilling til at beskrive en kurve, er vi – som det fremgår af figur 3 – ikke længere begræn­set af, at der til enhver x-værdi kun er én tilhørende y-værdi.

Videolektion