Linjer i rummet

Når man arbejder med linjer i rummet, bruger man stort set kun deres parameterfremstilling. I princippet kan man også opskrive en ligning for linjer i rummet, men det er en grim formel, som er svær at anvende i praksis. 

Parameterfremstillingen for linjen er stort set som i 2D bare med et tredje koordinat på retningsvektoren og det faste punkt.

Et punkt (x, y, z) ligger således på en ret linje, hvis det opfylder ligningen

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}+t\cdot\begin{pmatrix}r_1\\r_2\\r_3\end{pmatrix}$$

Dette kan også skrives som

$$\overrightarrow{OP}=\overrightarrow{OP_0}+t\cdot\overrightarrow{r}$$

Man kan også skrive parameterfremstillingen som funktioner for hver koordinat:

$$x=x_0+t\cdot r_1$$

$$y=y_0+t\cdot r_2$$

$$z=z_0+t\cdot r_3$$

Parameterfremstillingen for linjer i rummet fungerer på samme måde som i planen. Man starter i et punkt på linjen og derfra kan man nå alle punkter på linjen ved at gå en forlængelse/forkortelse af retningsvektoren ud fra punktet.

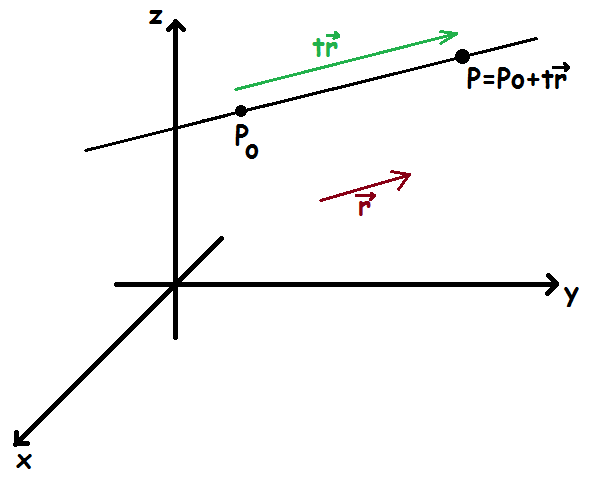
Et eksempel på en parameterfremstilling er

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}2\\3\\0\end{pmatrix}+t\cdot\begin{pmatrix}1\\1\\4\end{pmatrix}$$

Parameterfremstillingen beskriver en linje, der går gennem punktet (2, 3, 0) og har retningen

$$\overrightarrow{r}=\begin{pmatrix}1\\1\\4\end{pmatrix}$$