Vinkel mellem to planer

$Hvis man har to planer α og β, kan man beregne vinklen mellem dem.

Man starter med at finde vinklen mellem de to planers normalvektorer.
Dette gør man med den formel, vi kender fra 2D.

$$\cos(v)=\frac{\overrightarrow{n_\alpha}\cdot \overrightarrow{n_\beta}}{|\overrightarrow{n_\alpha}|\cdot|\overrightarrow{n_\beta}|}$$

Vinklen mellem normalvektorerne danner dog to vinkler, en stump og en spids, alt efter hvordan man definerer sine normalvektorer. Hvis vinklen v er vinklen mellem planerne, så vil vinklen mellem normalvektorerne i det spidsvinklede tilfælde også være v. I det stumpvinklede tilfælde vil vinklen mellem normalvektorerne være u, hvoraf vinklen mellem planerne, v, findes ved \( v=180^\circ-u \).

Man kan illustrere det stumpvinklede tilfælde ved hjælp af følgende tegning. Tegningen er kun 2D, men man kan forestille sig, at det er tværsnittet af to planer i rummet. 

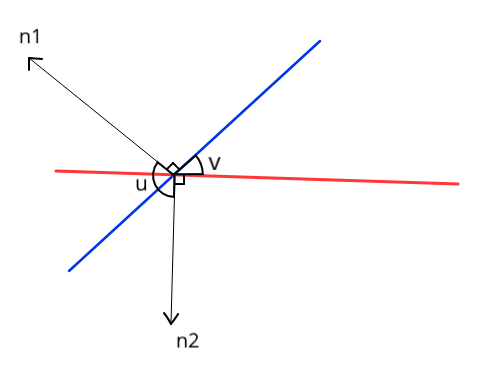
Her ses den stumpe vinkel, u, mellem de to normalvektorer, n1 og n2. Man finder vinklen mellem de to planer, rød og blå linje, ved \( 180^\circ - u \).

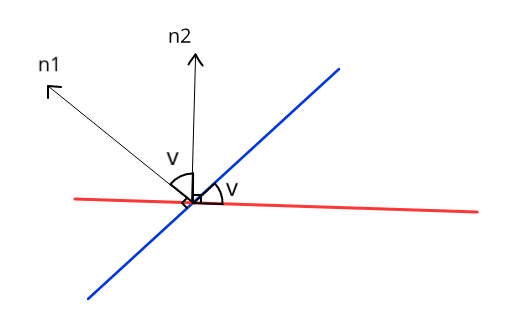
Det spidsvinklede tilfælde kan ses nedenfor. Her ses det, at den spidse vinkel mellem de to normalvektorer er lig vinklen mellem planerne.