Differentiation af vektorfunktion

Hvis vi betragter kurven hørende til en vektorfunktion som en partikels bevægelsesbane, kan vi være interesserede i at bestemme partiklens hastighed og acceleration.

Her benytter vi vores viden om differentiation af funktioner. Vi antager, at både $x(t)$ og $y(t)$ i parameterfremstillingen er differentiable mht. $t$.

I figur 12 ser vi på partiklens position til tiden $t_0$ og $t_0+dt$. Da både $x(t)$ og $y(t)$ er differentiable mht. $t$, gælder:

$x’(t)=\dfrac{dx}{dt}$ og $y’(t)=\dfrac{dy}{dt}$

Ved at gange igennem med $dt$ fremkommer:

$dx=x’(t)\cdot dt$ og $dy=y’(t)\cdot dt$

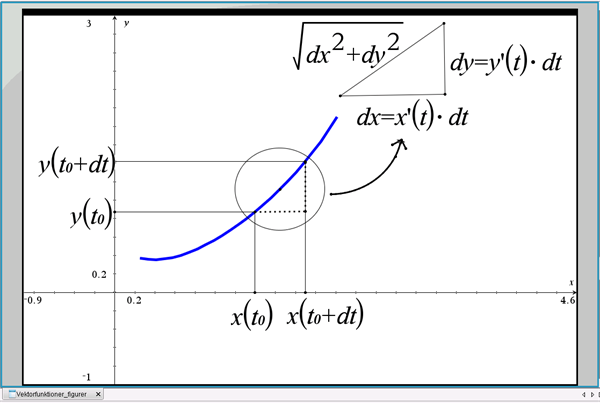
Figur 12    Differentiation af vektorfunktion

Vi kan bestemme kurvens hældning – og dermed tangentens hældning – i punktet $(x_0,y_0)$:

hældning $= \dfrac{dy}{dx} = \dfrac{y’(t_0)}{x’(t_0)}$

Vi kan bestemme partiklens hastighedsvektor, som også er retningsvektor for tangenten til banekurven:

$\overrightarrow{v(t_0)}=(x’(t_0), y’(t_0))$

Partiklens fart er da længden af hastighedsvektoren:

$|\overrightarrow{v(t_0)}|=\sqrt{x’(t_0)^2+y’(t_0)^2}$

Fra bevægelseslæren ved vi, at accelerationen fremkommer ved differentiering af hastigheden, så partiklens accelera­tionsvektor er:

$\overrightarrow{a(t_0)}=(x’’(t_0), y’’(t_0))$

og længden af accelerationsvektoren er:

$|\overrightarrow{a(t_0)}|=\sqrt{x’’(t_0)^2+y’’(t_0)^2}$

Eksempel 1

For en cirkulær banekurve med centrum i (0,0) er:

$(x(t),y(t))=(r\cdot\cos(\omega t), r\cdot\sin(\omega t))$ og

$(x’(t),y’(t))=(-\omega r\cdot\sin(\omega t), \omega r\cdot\cos(\omega t))$ og

$(x’’(t),y’’(t))=(-\omega ^2r\cdot\cos(\omega t), -\omega ^2r\cdot\sin(\omega t))$, hvor

$r$ er radius (meter), vinkelhastigheden $\omega = \frac{2\pi}{T}$ (rad/sek) og $T$ er omløbstiden (sek).

Partiklens hastighed er konstant og følger overalt tan­gentens retning, der er vinkelret på radius til partiklens aktuelle position:

$|\overrightarrow{v(t)}|=\sqrt{x’(t)^2+y’(t)^2}=\omega\cdot r$ (m/s)

Partiklens acceleration er ligeledes konstant og har retning fra partiklens aktuelle position ind mod cirklens centrum med længden:

$|\overrightarrow{a(t)}|=\sqrt{x’’(t)^2+y’’(t)^2}=\omega ^2\cdot r$ (m/s²)

Eksempel 2

For en ellipseformet banekurve med centrum i (0,0) er:

$(x(t),y(t))=(a\cdot\cos(\omega t), b\cdot\sin(\omega t))$ og

$(x’(t),y’(t))=(-\omega a\cdot\sin(\omega t), \omega b\cdot\cos(\omega t))$ og

$(x’’(t),y’’(t))=(-\omega ^2a\cdot\cos(\omega t), -\omega ^2b\cdot\sin(\omega t))$, hvor

$a,b$ er ellipsebanens akser (meter) i hhv. x-retningen og y-retningen, den gennemsnitlige vinkelhastighed $\omega = \frac{2\pi}{T}$ (rad/sek) og $T$ er omløbstiden (sek).

Bemærk, at accelerationsvektoren - ligesom for cirklen - har retning fra partiklens aktuelle position ind mod ellipsens centrum.

Partiklens hastighed og acceleration er:

$|\overrightarrow{v(t)}|=\sqrt{x’(t)^2+y’(t)^2}=\omega\cdot a\cdot\sqrt{\sin^2(\omega t)+(\dfrac{b}{a})^2\cdot\cos^2(\omega t)}$ (m/s)

$|\overrightarrow{a(t)}|=\sqrt{x’’(t)^2+y’’(t)^2}=\omega^2\cdot a\cdot\sqrt{\cos^2(\omega t)+(\dfrac{b}{a})^2\cdot\sin^2(\omega t)}$ (m/s²)

Partiklens hastighed er størst omkring lilleaksens poler (hvis $a>b$: på y-aksen i hhv. $+b$ og $-b$), og partiklens acceleration er størst omkring storaksens poler (hvis $a>b$: på x-aksen i hhv. $+a$ og $-a$).