Krydsprodukt
Når man har med 3D-vektorer at gøre, findes der en ny regneart. Den kaldes krydsproduktet eller vektorproduktet. Man krydser to vektorer med hinanden på følgende måde
$$\overrightarrow{a}\times\overrightarrow{b}=\begin{pmatrix}\begin{vmatrix}a_2 & b_2\\a_3 & b_3\end{vmatrix}\\-\begin{vmatrix}a_1&b_1 \\a_3& b_3\end{vmatrix}\\\begin{vmatrix}a_1 & b_1\\a_2 & b_2\end{vmatrix}\end{pmatrix}=\begin{pmatrix}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{pmatrix}$$
Bemærk, at når man krydser to vektorer med hinanden, så får man en ny vektor.
Huskeregel
Der findes en måde, så det er lettere at huske, hvordan man udregner krydsproduktet.
Når man skal finde førstekoordinatet i krydsproduktsvektoren, så holder man en hånd over de to førstekoordinater og udregner determinanten af det tiloversblevne.
Når man skal udregne andenkoordinatet, holder man for de to andenkoordinater og udregner determinanten af det tiloversblevne. Når man har gjort det skal man huske at sætte et minus foran!
Når man skal udregne tredjekoordinatet i krydsproduktsvektoren holder man for tredjekoordinaterne
og tager determinanten af det synlige.
Vi illustrerer huskereglen ved et eksempel.
Vi ønsker at udregne krydsproduktet
$$\begin{pmatrix}1\\2\\3\end{pmatrix}\times\begin{pmatrix}4\\5\\6\end{pmatrix}$$
Vi holder en hånd over førstekoordinaterne og finder determinanten af de fire tal, der er synlige
$$\begin{vmatrix}2 & 5\\3 & 6\end{vmatrix}=2\cdot6-3\cdot5=12-15=-3$$
førstekoordinatet er altså -3
Nu holder vi for andenkoordinaterne og finder determinanten af de fire synlige tal
$$\begin{vmatrix}1 & 4\\3 & 6\end{vmatrix}=1\cdot6-3\cdot4=6-12=-6$$
Ved andenkoordinatet skal man huske at sætte minus foran! Så andenkoordinatet bliver altså 6
Til sidst holder vi en hånd over tredjekoordinaterne og udregner determinanten af de fire synlige tal
$$\begin{vmatrix}1 & 4\\2 & 5\end{vmatrix}=1\cdot5-2\cdot4=5-8=-3$$
Krydsproduktet giver altså
$$\begin{pmatrix}1\\2\\3\end{pmatrix}\times\begin{pmatrix}4\\5\\6\end{pmatrix}=\begin{pmatrix}-3\\6\\-3\end{pmatrix}$$
Egenskaber ved krydsproduktet
Når man finder krydsproduktet af to vektorer, vil krydsproduktsvektoren stå vinkelret på begge de to oprindelige vektorer.
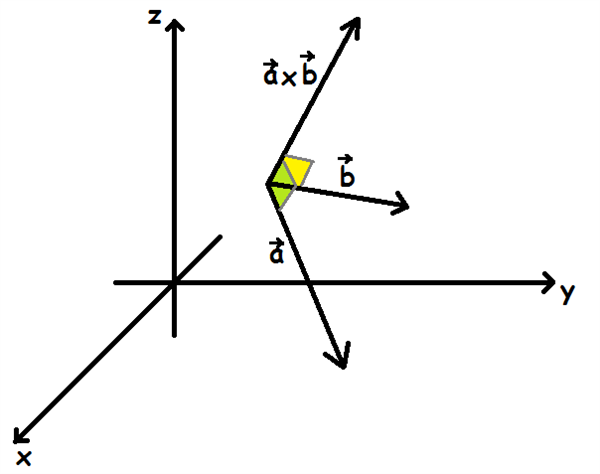
Vi kan tjekke, at det er rigtigt i eksemplet ovenfor ved at prikke hver af vektorerne sammen med krydsproduktsvektoren
$$\begin{pmatrix}1\\2\\3 \end{pmatrix}\cdot\begin{pmatrix}-3\\6\\-3\end{pmatrix}=1\cdot(-3)+2\cdot6+3\cdot(-3)=-3+12-9=0$$
$$\begin{pmatrix}4\\5\\6\end{pmatrix}\cdot\begin{pmatrix}-3\\6\\-3\end{pmatrix}=4\cdot(-3)+5\cdot6+6\cdot(-3)=-12+30-18=0$$
Da begge prikprodukter giver 0, betyder det at hver af vektorerne er ortogonale med krydsproduktet.
Areal af parallellogram
Udover at stå vinkelret på begge vektorer, så er længden af krydsproduktet lig med arealet af det parallellogram, der udspændes af de to vektorer.
$$A_{parallellogram}=|\overrightarrow{a}\times\overrightarrow{b}|$$
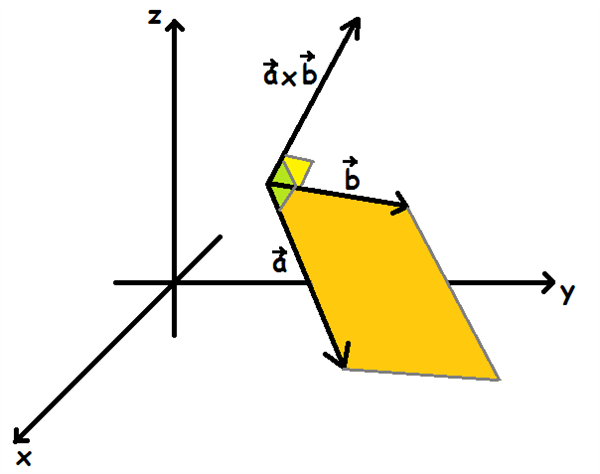
F.eks. kan arealet af parallelogrammet udspændt af vektorerne
$$\begin{pmatrix}1\\2\\3\end{pmatrix}\text{ og }\begin{pmatrix}4\\5\\6\end{pmatrix}$$
udregnes som:
$$
\begin{align}
\left | \begin{pmatrix}1\\2\\3\end{pmatrix} \times \begin{pmatrix}4\\5\\6\end{pmatrix} \right | = \left | \begin{pmatrix} -3\\ 6\\ -3 \end{pmatrix} \right | & = \sqrt{(-3)^2+6^2+(-3)^2}\\
&=\sqrt{9+36+9} = \sqrt{54} \\
& \approx 7,35
\end{align}
$$
Parallelle vektorer
Hvis krydsproduktet af to vektorer giver nulvektoren, betyder det, at de to vektorer er parallelle.
$$\overrightarrow{a}\times\overrightarrow{b}=\overrightarrow{0}\quad\Leftrightarrow\quad\overrightarrow{a}\parallel\overrightarrow{b} \ .$$
Dette skyldes, at længden af krydsproduktet mellem to vektorer kan skrives som
$$ |\overrightarrow{a}\times\overrightarrow{b}| = | \overrightarrow{a} | \cdot | \overrightarrow{b} | \sin(v) \ , $$
hvor \( v \) er den udspændte vinkel mellem de to vektorer. Da \( \sin(0) = \sin(\pi) = 0\) betyder det altså, at hvis de to vektorer er enten ensrettede eller modsatrettede parallelle, så er længden af deres krydsprodukt nul. Da længden af krydsproduktet er givet som kvadratroden af en sum af positive størrelser medfører det altså at hvis længden er nul, må krydsproduktet nødvendigvis også være det.
