Radianer

Vi har været vant til at måle vinkler i grader. I dette tilfælde er der 360 grader rundt på en cirkel. I mange tilfælde kan det være nyttigt at måle vinkler i radianer. Skal man f.eks. differentiere de trigonometriske funktioner, kan det kun lade sig gøre, hvis man måler vinklerne i radianer. En vinkels radiantal er defineret som forholdet mellem vinklens buelængde og cirklens radius.

$$\text{vinkel i radianer}=\frac{\text{buelængde}}{\text{radius}}$$

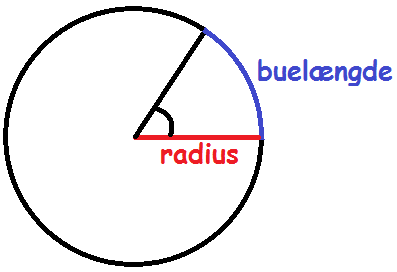
Hvis vi har at gøre med enhedscirklen, er radius 1. Derfor svarer vinklens radiantal til den buelængde, den spænder over på enhedscirklen.

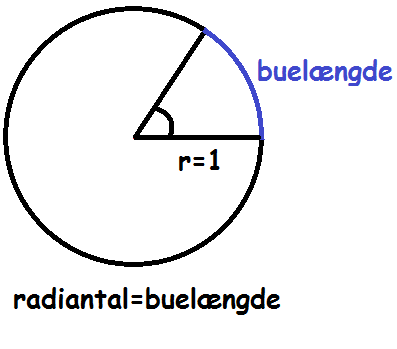
Da omkredsen af en cirkel er

$$O=2\pi r$$

må omkredsen af enhedscirklen være

$$O=2\pi\cdot1=2\pi$$

Derfor er der 2π radianer hele vejen rundt på en cirkel.
Vi kan opstille følgende tabel, der omregner radianer og grader

Grader	Radianer
\(0^{\circ}\)	\(0\)
\(30^{\circ}\)	\(\frac{\pi}{6}\)
\(45^{\circ}\)	\(\frac{\pi}{4}\)
\(60^{\circ}\)	\(\frac{\pi}{3}\)
\(90^{\circ}\)	\(\frac{\pi}{2}\)
\(180^{\circ}\)	\({\pi}\)
\(270^{\circ}\)	\(\frac{3\pi}{2}\)
\(360^{\circ}\)	\(2\pi\)

Hvis man skal omregne nogle vinkler, der ikke står i tabellen, kan man bruge følgende formler. Her er v vinklen målt i grader, og x er vinklen målt i radianer

$$x=\frac{v}{360^\circ}\cdot2\pi$$

$$v=\frac{x}{2\pi}\cdot360^\circ$$

Her er tegnet en enhedscirkel med de vigtigste vinkler tegnet ind