Længde af vektor

Når vi skal beregne længden af en vektor i 3D, bruger vi en formel der minder meget om 2D-formlen

$$|\overrightarrow{a}|=\sqrt{a_1^2+a_2^2+a_3^2}$$

Som et eksempel kan vi udregne længden af vektoren med koordinaterne 2, 4 og 6.

$$\left | \begin{pmatrix}2\\4\\6\end{pmatrix} \right |=\sqrt{2^2+4^2+6^2}=\sqrt{4+16+36}=\sqrt{56}\approx7,48$$

Hvis vi skal forklare, hvorfor formlen ser sådan ud, skal vi holde tungen lige i munden og gøre brug af Pythagoras to gange.

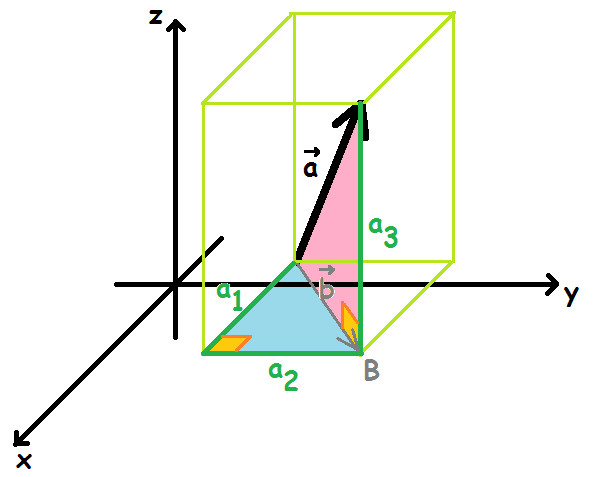
Fra slutpunktet af vektor a går vi lodret ned indtil vi når ned i samme højde som startpunktet. Dette punkt kalder vi B. Vi tegner vektoren b mellem startpunktet for vektor a og punktet B.

Nu kan vi se, at vektor a udgør hypotenusen i en retvinklet trekant (lyserød) med vektor b som den ene katete, og a₃ som den anden. Altså kan vi udregne længden af vektor a, hvis vi bare kender længden af vektor b.

Vektor b udgør imidlertid hypotenusen i en anden retvinklet trekant (lyseblå) med kateterne a₁ og a₂. Derfor kan vi udregne længden af vektor b vha. Pythagoras.

$$|\overrightarrow{b}|^2=|a_1|^2+|a_2|^2\\|\overrightarrow{b}|^2=a_1^2+a_2^2$$

Grunden til at vi brugte numeriske tegn om a₁ og a₂ var, at vi skulle bruge længderne af kateterne, og vi ikke vidste om koordinaterne var positive eller negative. Når vi sætter i anden, får vi imidlertid altid et positivt tal, hvorved vi kan ophæve de numeriske tegn.

Nu kan vi bruge Pythagoras til at udregne længden af vektor a

$$\overrightarrow{a}|^2={\color{Gray} |\overrightarrow{b}|^2}+|a_3|^2$$

$$={\color{Gray} a_1^2+a_2^2}+|a_3|^2$$

$$=a_1^2+a_2^2+a_3^2$$

$$|\overrightarrow{a}|=\sqrt{a_1^2+a_2^2+a_3^2}$$