Bestemt integral og areal
En af de vigtigste forskelle på det bestemte og det ubestemte integral er, at mens det ubestemte integral giver en funktion (nemlig stamfunktionen) så giver det bestemte integral et tal.
$$\int f(x)\,dx=\text{funktion}$$
$$\int_a^bf(x)\,dx=\text{tal}$$
De to tal a og b kaldes integrationsgrænserne. Man udregner et bestemt integral på følgende måde
$$\int_a^bf(x)\,dx=[F(x)]_a^b=F(b)-F(a)$$
Dette betyder, at man først finder en stamfunktion til f. Denne stamfunktion skriver man inde i kantede parenteser med de to integrationsgrænser til højre. Derefter sætter man den øvre integrationsgrænse (b) ind på x's plads, hvorefter man sætter den nedre integrationsgrænse (a) ind på x's plads og trækker fra.
Et eksempel kunne være.
$$\int_0^2\underbrace{6x^2}_{f(x)}\,dx=[\underbrace{2x^3}_{F(x)}]_0^2=\underbrace{2\cdot2^3}_{F(b)}-\underbrace{2\cdot0^3}_{F(a)}=16$$
Bemærk, at vi bare fandt en tilfældig stamfunktion til f uden at tænke på at lægge en integrationskonstant til. Sådan er det altid med bestemte integraler.
Areal
Ovenfor sagde vi, at det bestemte integral giver et tal. Nogle gange er dette tal lig med arealet mellem funktionen f og x-aksen i intervallet [a;b]. Men det er ikke altid. Det er kun hvis f er positiv på hele intervallet [a;b]. Dvs. at grafen for f ligger ovenover x-aksen på hele intervallet.
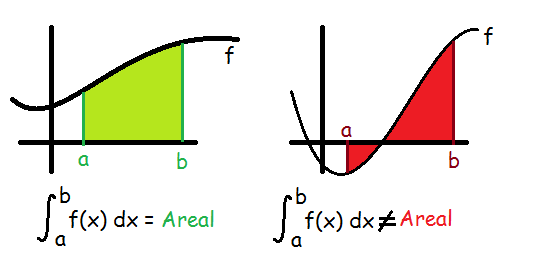
Lad os tage et eksempel. Vi ønsker at finde arealet af figuren M på nedenstående tegning.
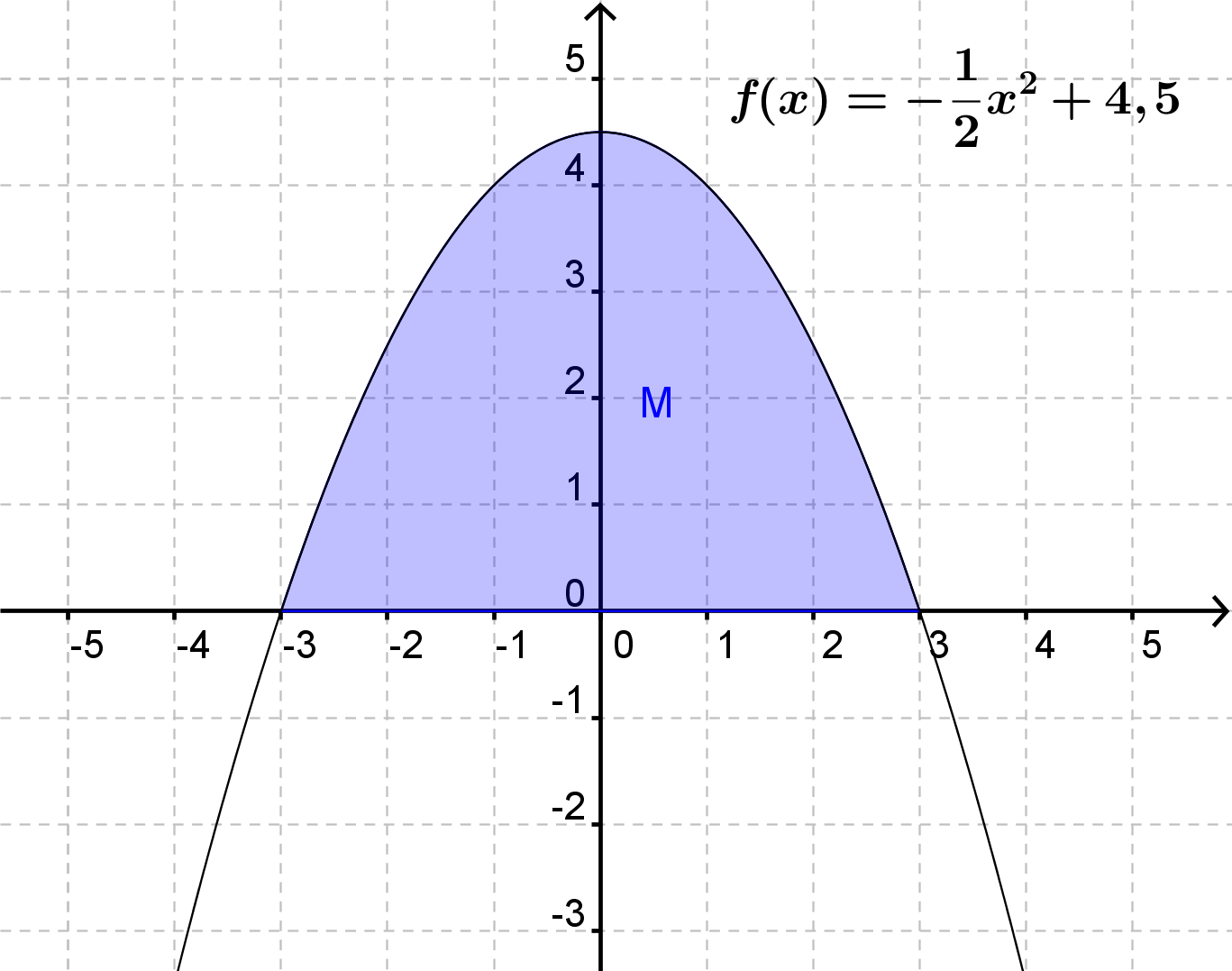
Vi kan se, at funktionen f er positiv (grafen ligger over x-aksen) på hele intervallet [-3;3].
Derfor vil det bestemte integral med integrationsgrænserne -3 og 3 give arealet af M.
$$Areal_M=\int_{-3}^3-\frac{1}{2}x^2+4,5\,dx=[-\frac{1}{2}\cdot\frac{1}{3}x^{2+1}+4,5x]_{-3}^3$$
$$=[\frac{-1}{6}x^3+4,5x]_{-3}^3=\frac{-1}{6}\cdot3^3+4,5\cdot3-(\frac{-1}{6}\cdot(-3)^3+4,5\cdot(-3))$$
$$=\frac{-27}{6}+13,5-(\frac{27}{6}-13,5)=\frac{-54}{6}+27=-9+27=18$$
Arealet af M er altså 18.
