Skæring mellem linje og kugle

Hvis man har en linje og en kugle i rummet, kan man være interesseret i at finde ud af, om de skærer hinanden.

Man finder frem til eventuelle skæringspunkter ved at indsætte koordinatfunktionerne fra linjens parameterfremstilling i kuglens ligning.

Dette vil give en andengradsligning, hvor t er den ubekendte.

Man beregner andengradsligningens diskriminant, og der er tre muligheder

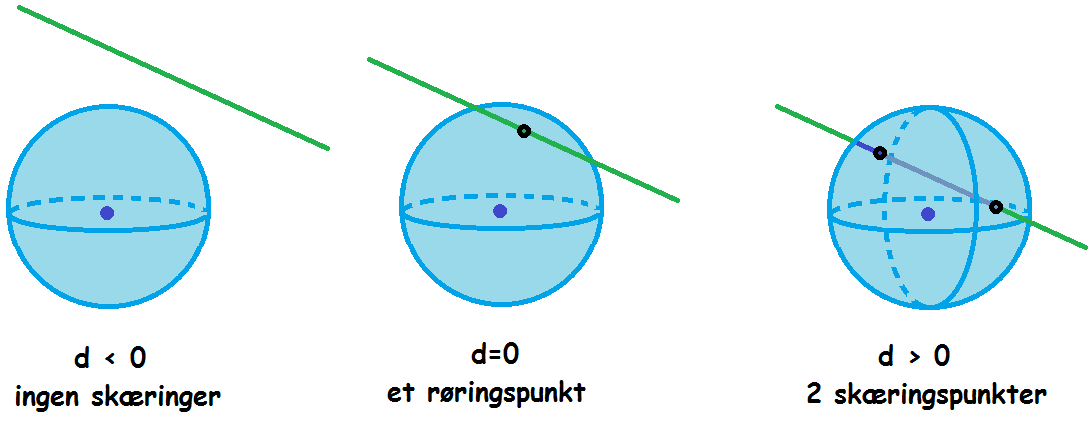
Hvis d ≥ 0, kan man finde frem til skæringspunkterne ved først at løse andengradsligningen, og dernæst indsætte de fundne t-værdier i linjens parameterfremstilling. Dermed vil man finde frem til røringspunkt/skæringspunkter.

Lad os tage et eksempel

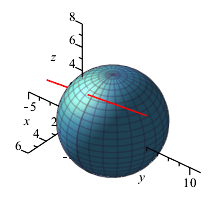
Vores kugle har r=4 og C(-1, 2, 0). Dens ligning er

$$\mathcal{K}:\:(x+1)^2+(y-2)^2+z^2=16$$

Vores linje har parameterfremstillingen

$$l:\:\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\1\\3\end{pmatrix}+t\cdot\begin{pmatrix}1\\2\\1\end{pmatrix}$$

Vi skriver hver enkelt koordinatfunktion op

$$x=1+t$$

$$y=1+2t$$

$$z=3+t$$

Nu sætter vi disse ind i kuglens ligning

$$((1+t)+1)^2+((1+2t)-2)^2+(3+t)^2=16$$

$$(t+2)^2+(2t-1)^2+(t+3)^2=16$$

$$(t^2+4+4t)+(4t^2+1-4t)+(t^2+9+6t)=16$$

$$6t^2+6t+14=16$$

$$6t^2+6t-2=0$$

Vi finder diskriminanten for andengradsligningen

$$d=b^2-4ac=6^2-4\cdot6\cdot(-2)=36+48=84$$

Da diskriminanten er større end 0, er der to skæringer mellem kuglen og linjen. 

Vi løser andengradsligningen

$$t=\frac{-b\pm\sqrt{d}}{2a}=\frac{-6\pm\sqrt{84}}{2\cdot6}\approx\frac{-6\pm9,17}{12}$$

$$t_1\approx0,26\qquad t_2\approx-1,26$$

Ved at indsætte disse t-værdier i linjens parameterfremstilling, når vi frem til skæringspunkterne.

$$\overrightarrow{OP_1}=\begin{pmatrix}1\\1\\3\end{pmatrix}+0,26\cdot\begin{pmatrix}1\\2\\1\end{pmatrix}=\begin{pmatrix}1,26\\1,52\\3,26\end{pmatrix}\\\overrightarrow{OP_2}=\begin{pmatrix}1\\1\\3\end{pmatrix}-1,26\cdot\begin{pmatrix}1\\2\\1\end{pmatrix}=\begin{pmatrix}-0,26\\-1,52\\1,74\end{pmatrix}$$

Altså har vi, at P₁(1.26, 1.52, 3,26) og P₂(-0.26, -1.52, 1.74) er de to skæringspunkter mellem kuglen og linjen.

Kuglen og linjen fra eksemplet er tegnet her