Skæring mellem linje og plan

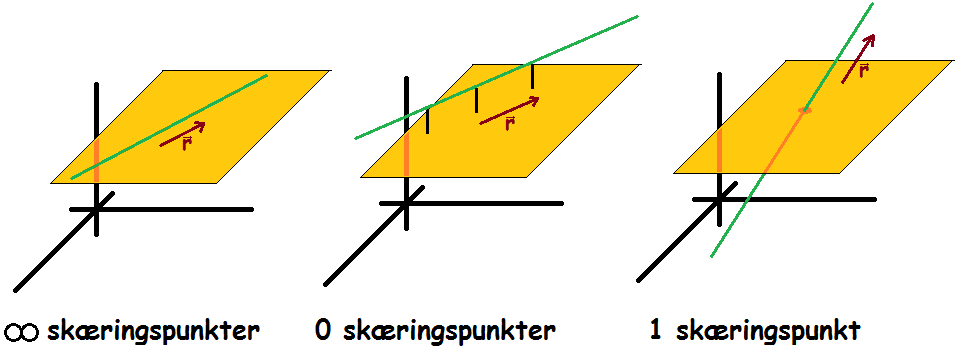
Når man skal se, hvordan linjer og planer forholder sig i forhold til hinanden, er der tre muligheder.

• Hvis linjen ligger i planen (dvs. at både retningsvektoren og det faste punkt ligger i planen), er der uendeligt mange skæringspunkter.

• Hvis linjens retningsvektor ligger i planen, men det faste punkt ikke gør, så er der ingen skæringer.

• Hvis linjens retningsvektor ikke ligger i planen, er der ét skæringspunkt.

Man kan undersøge om retningsvektoren ligger i planen ved at prikke den med planens normalvektor. Hvis prikproduktet giver 0, er de to vektorer ortogonale og det vil sige, at retningsvektoren ligger i planen (hvis planen er givet ved en parameterfremstilling og ikke en ligning, kan man finde normalvektoren ved at krydse planens to retningsvektorer med hinanden)

Hvis retningsvektoren ligger i planen, kan man undersøge om linjens faste punkt også ligger i planen. Det gør man ved at indsætte punktet i planens ligning og se, om den er opfyldt. (Hvis planen er givet ved en parameterfremstilling, sætter man punktet ind på venstre side og bruger to af de tre ligninger til at isolere s og t. Dernæst indsætter man s- og t-værdierne i den tredje for at undersøge om den er opfyldt).

Hvis retningsvektoren ikke ligger i planen, kan man beregne skæringspunktets koordinater.

Find skæring, når plan er givet ved ligning

Hvis planen er givet ved en ligning og linjen ved parameterfremstilling, så finder man skæringen mellem dem på følgende måde:

Først indsætter man hver enkelt koordinatfunktion fra linjen i planens ligning. Dernæst isolerer man t. Den fundne t-værdi indsættes slutteligt i linjens parameterfremstilling, og det punkt, man når frem til er skæringspunktet.

Lad os tage et eksempel:

$$l:\quad\begin{pmatrix}x\\y\\z \end{pmatrix}=\begin{pmatrix} 1\\ 5\\ 0 \end{pmatrix}+t\cdot\begin{pmatrix} 2\\ -2\\ 1 \end{pmatrix}$$

$$\alpha:\quad 2x+3y-z+4=0$$

Vi kan skrive linjens parameterfremstilling om til de tre koordinatfunktioner

$$x=1+2t$$

$$y=5-2t$$

$$z=0+t=t$$

Disse funktioner sætter vi så ind på x's, y's og z's pladser i planens ligning

$$2(1+2t)+3(5-2t)-(0+t)+4=0$$

$$2+4t+15-6t-t+4=0$$

$$-3t+21=0$$

$$t=\frac{21}{3}=7$$

Vi har altså fundet ud af, at linje og plan skærer hinanden, når t=7. Nu mangler vi bare at indsætte t=7 i linjens parameterfremstilling for at finde frem til skæringspunktet

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\5\\0\end{pmatrix}+7\cdot\begin{pmatrix}2\\-2\\1\end{pmatrix}=\begin{pmatrix}1+7\cdot2\\5-7\cdot2\\0+7\cdot1\end{pmatrix}=\begin{pmatrix}15\\-9\\7\end{pmatrix}$$

Skæringspunktet er derfor (15, -9, 7)

Find skæring, når plan er givet ved parameterfremstilling

Hvis planen er givet ved en parameterfremstilling, kan man enten omskrive parameterfremstilingen til en ligning og gøre som ovenfor, eller man kan løse tre ligninger med tre ubekendte.

Lad os tage et eksempel

$$l:\quad\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}0\\0\\1\end{pmatrix}+u\cdot\begin{pmatrix}2\\-1\\1\end{pmatrix}\quad\Leftrightarrow\quad\begin{matrix}x=2u\\y=-u\\z=1+u\end{matrix}$$

$$\alpha:\quad\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\1\\2\end{pmatrix}+s\cdot\begin{pmatrix}1\\2\\0\end{pmatrix}+t\cdot\begin{pmatrix}3\\0\\1\end{pmatrix}\quad\Leftrightarrow\quad\begin{matrix}x=1+s+3t\\y=1+2s\;(+0\cdot t)\\z=2+t\;(+0\cdot s)\end{matrix}$$

Bemærk, at vi har givet alle parametrene forskellige navne, således at linjens parameter hedder u, mens planens hedder s og t.

Nu sætter vi ligningerne for x lig hinanden, ligningerne for y lig hinanden og ligningerne for z lig hinanden.

$$2u=1+s+3t$$

$$-u=1+2s$$

$$1+u=2+t$$

Vi starter med at isolere en af parametrene i en af ligningerne. Lad os isolere u i den tredje ligning

$$u=2+t-1=1+t$$

Dette sætter vi nu ind på u's plads i de andre ligninger

$$2(1+t)=1+s+3t$$

$$-(1+t)=1+2s$$

Nu står vi med to ligninger med to ubekendte. Vi isolerer s i den øverste

$$s=2(1+t)-1-3t=2+2t-1-3t=1-t$$

Dette sætter vi nu ind på s's plads i den anden ligning

$$-(1+t)=1+2(1-t)$$

$$-1-t=1+2-2t$$

$$-t+2t=1+2+1$$

$$t=4$$

Nu ved vi at t=4, og vi kan indsætte dette i udtrykkene for u og s

$$u=1+t=1+4=5$$

$$s=1-t=1-4=-3$$

Nu indsætter vi enten u-værdien i linjens parameterfremstilling eller s- og t-værdierne i planens parameterfremstilling. Lige meget i hvilken vi indsætter, når vi frem til skæringspunktet. Vi indsætter u=5 i linjens parameterfremstilling

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}0\\0\\1\end{pmatrix}+5\cdot\begin{pmatrix}2\\-1\\1\end{pmatrix}=\begin{pmatrix}0+5\cdot2\\0+5\cdot(-1)\\1+5\cdot1\end{pmatrix}=\begin{pmatrix}10\\-5\\6\end{pmatrix}$$

Altså skærer linjen planen i punktet (10, -5, 6).