Feriedestination Barcelona
Rigtig mange danskere rejser hvert år til storbyer som Paris, Barcelona og London.
Matematikcenter har set nærmere på, hvor der er matematik i disse feriedestinationer, så du har nogle funfacts at imponere familien eller vennerne med på turen.
Vidste du for eksempel, at franske matematikeres navne er indgraveret i Eiffeltårnet, og at Sagrada Familias lysskakter er udformet som hyperboloider? Eller at tiden går en lillebitte smule hurtigere, når du er oppe i London Eye?
Barcelona
Katedralen Sagrada Familia har været under konstruktion siden 1882 og forventes færdig om 10 år.
Arkitekten Antoni Gaudi arbejde på kirken fra 1884 til han døde i 1926. Katedralen har 18 tårne, der hver symboliserer enten apostlene, evangelisterne, Jesus eller Jomfru Maria. I sådan et byggeri er der naturligvis rigtig meget geometri.
Det ses fx i katedralens trappeopgange, lysskakter, søjler og søjlehoveder.
Vi vil se nærmere på lysskakterne, der er opbygget som hyperboloider.
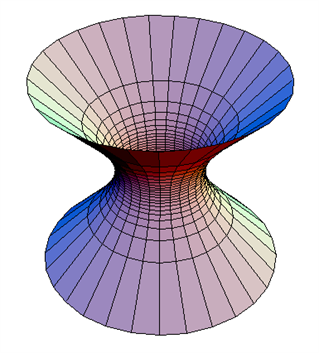
Hyperboloiden med ét net (som der er tale om her) kan beskrives med funktionen
$$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$$
I tilfældet med lysskakterne i Sagrada Familia er a=b, og det kaldes en omdrejningshyperboloide.
For at forstå, hvordan hyperboloider fremkommer, kan du forestille dig følgende:
En cylinder består af en cirkel i toppen og en cirkel i bunden, som er forbundet af uendeligt mange linjestykker, der danner cylinderens krumme overflade. Hvis den ene cirkel drejes om centrum, vil disse linjestykker, der stadig er rette, omdanne cylinderen til en hyperboloide.
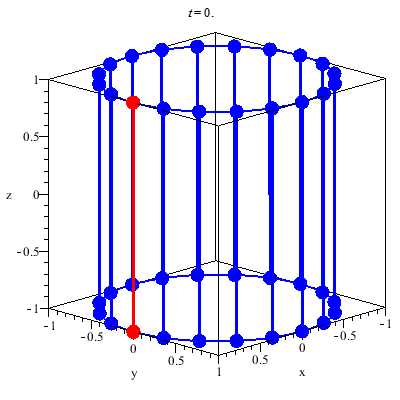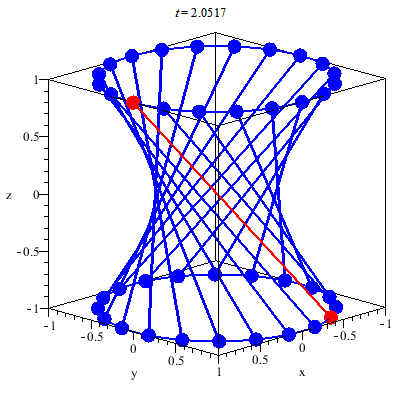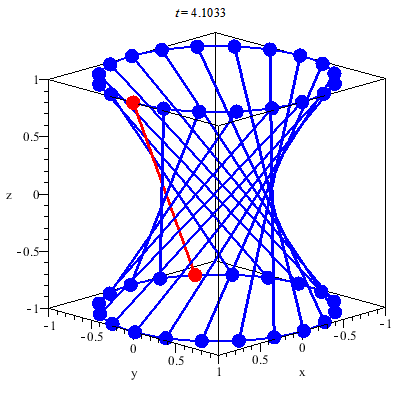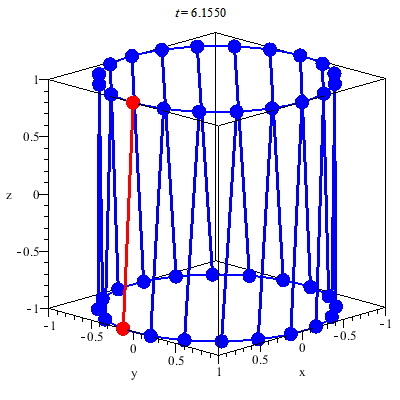
Disse linjestykker kaldes hyperboloidens frembringere, og alt efter hvilken vej den ene cirkelskive drejes, kaldes de enten højrefrembringere eller venstrefrembringer (alt efter om de hælder til højre eller til venstre).
Frembringelsen af en hyperboloide svarer til, at man roterer en hyperbel om z-aksen i et 3D-koordinatsystem. Det sted, hvor figuren er smallest, kaldes strubecirklen. Det er altså størrelsen af strubecirklen, der er begrænsende for, hvor meget lys der kan komme ned gennem lysskakterne i Sagrada Familias loft.
Kilder
https://en.wikipedia.org/wiki/Eiffel_Tower
https://en.wikipedia.org/wiki/List_of_the_72_names_on_the_Eiffel_Tower
http://www.sagradafamilia.org/en/geometry/
https://da.wikipedia.org/wiki/Massefylde
https://en.wikipedia.org/wiki/Sagrada_Fam%C3%ADlia
http://mimimi.dk/bcn/ivan/Barcelona_kursus_sept_2010/Gaudi_geometri_09.pdf
https://en.wikipedia.org/wiki/London_Eye
"Gaudis arkitektur med TI-Nspire CAS" af Bjørn Felsager, 2013
"Physical Mathematics" af Kevin Cahill, 2013
