Solen

Sommeren og solen er over os - på trods af en lidt dansk sommer. Solen bringer energi til jorden og styrer derved hvilken temperatur luften og jorden har. Men hvorfor er det egentlig varmere om sommeren end om vinteren? Og hvor hurtigt kan solen få 1 liter vand i kog?

Sommervarmen

Hvis jordens akse var lodret, ville sommer og vinter have samme temperatur. Men eftersom jordens akse hælder skråt, føles solen varmere om sommeren i Danmark. Det skyldes at solens stråler går mere lodret ned imod jorden om sommeren end om vinteren, og der modtages derfor mere energi pr. m². Forskellen fra vinter til sommer mærkes også i dagens længde. På grund af daglængden, modtager vi også mere energi om sommeren end om vinteren.

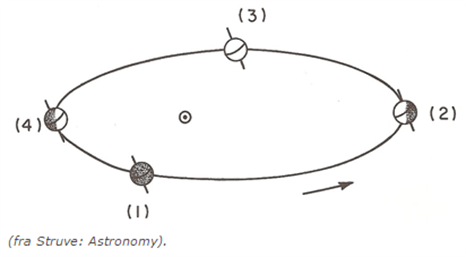
På figuren ses jordens bane omkring solen. Ved tegning nr. 2 vises jorden i den position den har om sommeren. Ved tegning nr. 4 vises jordens position i forhold til solen om vinteren. Jordens bane er en lille smule elliptisk og der er derfor en lidt varmere sommer på den sydlige halvkugle end på den nordlige. Jorden er nemlig tættest på solen om vinteren og lidt længere væk fra solen om sommeren.

Hvis solen var en elkedel

Temperaturen i solens kerne når op på 15,5 millioner grader, mens dens overflade er 5500 grader. Solens samlede effekt er 3,846*10²⁶ W og holder man 1 liter vand på 20 °C hen til den, tager det kun fire kvadrilliontedele af et sekund at få vandet i kog!

Sådan har vi regnet den ud:

Den nødvendige varmemængde Q, der skal tilføres vandet, er lig med produktet af følgende faktorer: Vandets masse m, den specifikke varmekapacitet c og temperaturændringen ΔT. Det regnes således:

$$Q=m\cdot c\cdot \Delta T\\=1\text{ kg}\cdot 4184\frac{\text{ J}}{\text{ kg}\cdot ^{\circ}\text{C}}\cdot \left ( 100 ^{\circ}\text{C}-20^{\circ}\text{C}\right )\\=334720\text{ J}\\=334,\!720\text{ kJ}$$

når vi regner med en nyttevirkning på 100%.

Endelig kan den nødvendige opvarmningstid t udregnes som forholdet mellem solens effekt P og den nødvendige energi Q.

$$t=\frac{\text{ Q}}{\text{ P}}=\frac{334720\text{ J}}{3,\!846\cdot 10^{26}\text{ W}}= 3,\!9565\cdot 10^{-24}\text{ sekunder}$$

Det svarer til fire kvadrilliontedele af et sekund!

 

Kilder

http://www.nbi.ku.dk/spoerg_om_fysik/astrofysik/aarstider/

http://www.denstoredanske.dk/It,_teknik_og_naturvidenskab/Astronomi/Solen/Solen

http://cubus-adsl.dk/elteknik/faq/watt_koge_vand.php

https://da.wikipedia.org/wiki/SI-pr%C3%A6fiks