Lego

Siden Lego indførte deres nuværende design af klodser i 1958, er der blevet produceret mere end 600 mia. Lego-klodser. Det er nok klodser til, at hver enkelt dansker kan få hele 105569 klodser. Med det antal kan man bygge et Lego-tårn, der er mere end 1 kilometer højt. Højere end verdens højeste bygning Burj Khalifa, der bare er 828 meter høj.

Det lyder af meget. Men hvis man samler alle Lego-klodserne kan man faktisk bygge et tårn, der kan nå hele vejen til månen og tilbage 7,5 gange. Og deres rumfang ville være det samme som hele 898 Rundetårne.

Sådan har vi regnet det

Som nævnt er der produceret 600.000.000.000 Lego-klodser. I Danmark bor der 5.683.480 mennesker. Hvis Lego klodserne skulle fordeles ligeligt ville hver dansker kunne få:
\(\frac{600\ 000\ 000\ 000\,\mathrm{klodser}}{5\ 683\ 480\,\mathrm{mennesker}} = 105569 \) klodser per person.  

Tårn

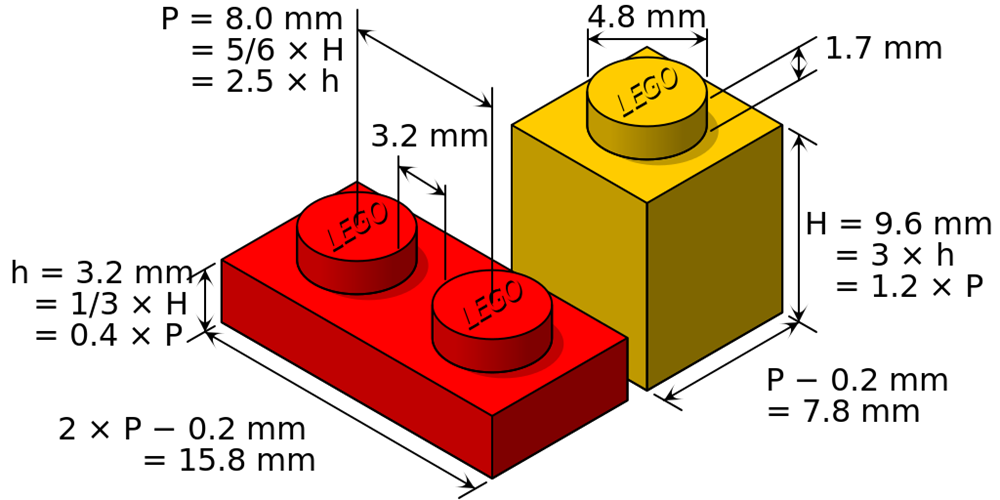
Højden på en Lego-klods er 9,6 mm. Så med 105569 klodser kan hver dansker bygge et tårn på hele:
\(0{,}0096\,\mathrm{m/klods}\cdot 105569\, \mathrm{klodser} = 1013{,}5\, \mathrm{m}\)

 
Hvis man samler samtlige brikker kan man bygge et tårn der kan nå fra månen og tilbage 7,5 gange.  
Højden på tårnet vil blive:
\(0{,}0096\,\mathrm{m}\cdot 600\ 000\ 000\ 000\,\mathrm{klodser} = 5{,}76\; 10^9 \, \mathrm{m} \)
 
Afstanden til månen er 384400000 meter. Vi skal både frem og tilbage derfor:
\(2\cdot 384\ 400\ 000\, \mathrm{m} = 768\ 800\ 000\, \mathrm{m} \)
 
Nu kan vi bestemme hvor mange gange man kan nå til månen og tilbage:
\(\frac{5{,}76\; 10^9 \, \mathrm{m}}{768\ 800\ 000\, \mathrm{m}} = 7{,}5\)

Rundetårn

Rumfanget af en Legoklods kan bestemmes ud fra dens dimensioner. Vi har ikke kunnet finde information om, hvor mange klodser, der er produceret i hver størrelse, så vi antager, at den gennemsnitlige Legoklods er 4x2. Den har en højde på 9,6 mm, en længde på 31,2 mm og en bredde på 15,6 mm.
Rumfanget er altså:
\(0{,}0312\,\mathrm{m}\cdot 0{,}0156\,\mathrm{m}\cdot 0{,}0096\,\mathrm{m} = 0.47\; 10^{-5} \,\mathrm{m}^3 \)

Rumfanget af alle Lego-klodser produceret er altså:

\( 0.47\; 10^{-5} \,\mathrm{m}^3\mathrm{/klods} \cdot 6 \; 10^{11}\, \mathrm{klodser} = 2.8 \;10^6 \,\mathrm{m}^3\)

Rumfanget af Rundetårn er 3121.5 m\(^3\). Altså er antallet af Rundetårne man kan fylde op:

\(\frac{2.8 \;10^6 \,\mathrm{m}^3}{3121.5 \,\mathrm{m}^3} = 898\)