Tilbud på McDonald's
McDonald's Dammark lagde forleden et billede ud på deres facebook-side med et regnestykke, så man selv kunne regne tilbudsprisen på en Big Mac ud. Billedet kan ses her.

Regnestykket var \(3(1+2\cdot 3)+ 4kr. \), og tilbuddet lyder på, at man kan få en Big Mac til 25 kr.
Men lad os lige prøve at se på regnestykkets enhed: Hvis vi udregner stykket, så får vi 4 kr. + 21. Vi kan ikke bare lægge de to tal sammen, da de 21 ikke har nogen enhed. Man kan sige, at det er underforstået, at der er tale om 21 kr., men det er god skik alligevel at oplyse, hvad enheden er. Et tal bør i sådan en sammenhæng aldrig stå uden enhed, da vi jo teknisk set ikke ved, om der er tale om kroner, karmapoint eller kalahaspil.
Hvis man skal lægge to led sammen, kræves det at de har samme enhed.
Det betyder, at vi eksempelvis ikke kan lægge a'er og b'er sammen, meter og kilometer eller æbler og blommer.
Men hvordan kunne McDonald's have stillet regnestykket op, for at det skulle være entydigt, hvad de mente? Der er to muligheder:
1. De kunne indføre endnu enhed, så der kom til at stå \(3(1 kr.+2\cdot 3 kr.)+ 4kr. \)
2. De kunne sætte et ekstra sæt parentereser, så der kom til at stå \((3(1+2\cdot 3)+ 4)kr. \)
Begge muligheder giver en pris på 25 kr.
I kommentarerne til billedet er der mange, der har regnet prisen ud til at være 25 kroner, men der er også personer, der får prisen til fx 14 kr.,15 kr, 19 kr. og 28. kr.
Hvis man ikke får resultatet til 25 kroner, kan det skyldes, at man ikke kan huske regnearternes hierarki, hvor man allerførst skal udregne parenteser, hvorefter udregner rødder og potenser. Herefter ganger og dividerer man, og til sidst kan man lægge tal sammen og trække dem fra hinanden. Regnearternes hierarki gælder også inden i parenteser.
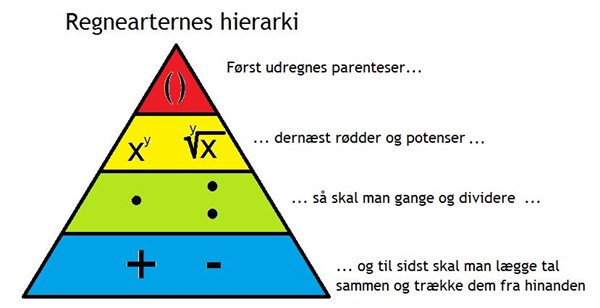
Lad os se på, hvordan regnearternes hierarki skal bruges i dette tilfælde. Vi tager udgangspunkt i stykket skrevet på formen \((3(1+2\cdot 3)+ 4)kr. \)
Regnearternes hierarki siger, at vi først skal udregne parenteser, så vi starter med at se på den inderste parentes. Her står der \(1+2\cdot 3\), og alle tallene er uden enhed. Vi skal starte med at gange, før vi lægger tal sammen: \(2\cdot 3= 6\).
Efter vi har ganget, kan vi udregne 6+1 = 7. Så er den inderste parentes udregnet, og vi har fået udtrykket \((3 \cdot 7+ 4)kr. \). Man skal altid huske, at når der står et tal foran en parentes, så skal det ganges på parentesens indhold, medmindre der står et "+" eller et "-". Det er altså \((3 \cdot 7+ 4)kr. \) og ikke \((3 + 7+ 4)kr. \). Så ser vi på \((3 \cdot 7+ 4)kr. \), og vi skal selvfølgelig gange, før vi lægger sammen, så vi får \(3 \cdot 7 = 21 \). Regnestykket er nu reduceret til \( (21 + 4)kr.\). Vi udregner, at 21+4 = 25, så vi får (25)kr. = 25 kr.
Med denne viden er du nu altid i stand til at udregne prisen på din burger og vurdere, og der er brugt de rigtige regneregler og enheder.
