NCC Materialeberegning

Entreprenørvirksomheden NCC har siden 2015 været Matematikcenters hovedsponsor. I Matematikcenter vil vi skabe begejstring og bedre forståelse for matematik og naturvidenskab blandt børn og unge. Gennem samarbejdet med NCC vil vi vise potentialet i en erhvervsrettet eller teknisk uddannelse.

Få styr på materialerne

Når du som tømrer, murer, struktør, osv., skal i gang med en opgave, er det vigtigt, at du får den korrekte mængde materialer med til opgaven. Har du for lidt, spilder du tid ved at hente mere. Har du for meget, spilder du tid ved at slæbe det overskydende tilbage. Desuden sparer du også din krop, ved ikke at slæbe for meget materiale frem og tilbage. Endeligt slipper du for at betale for det overskydende.

I videoen nedenfor, fortæller Daniel om, hvordan han håndterer materialeberegningen, når han skal sætte gipsvægge op.

 

 Et eksempel

Vi forestiller os en lejlighed, som er ved at blive renoveret. Daniel skal bestemme, hvor mange plader gips han skal bruge til opgaven. En skitse af lejligheden kan ses nedenfor.

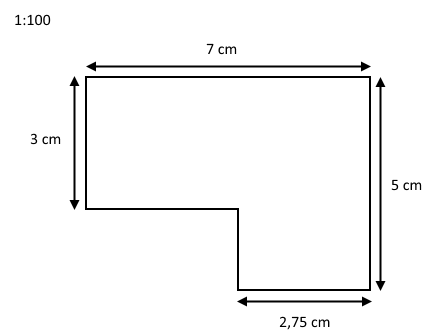
Målestok
Det første, man skal bemærke sig, er målestoksforholdet: 1:100. 1cm på tegningen svarer til 100cm i virkeligheden. Læs mere om målestoksforhold .

Når vi kender målestoksforholdet, kan vi hurtigt omregne cm til m på tegningen. I videoen siger Daniel, at én gipsplade er lidt over \(2m^2 \) i areal. Vi lader som om, en gipsplade er præcis \(2m^2 \), da det er nemmere at regne med. 

Væggenes areal
Vi starter med at regne ud, hvor stort et areal der skal beklædes med gips: 

Alle væggene skal have to lag gips på, mens loftet kun skal have et enkelt lag. For at finde arealet af væggene skal vi kende højden (fra gulv til loft) og længden (væg til væg). Der er ikke angivet en højde på tegningen, så vi antager, at højden er 3m. 

Først lægger vi alle væggenes længder sammen:

$$ 7m+2.75m+3m+5m = 17.75m$$

Nu kan vi gange det med 3m - højden til loftet:

$$ 17.75m \cdot 3m = 53.25m^2 $$

Loftets areal
For loftet er vi nødt til at inddele rummet i to firkanter.
Den store firkant er 7m i længden og 3m i bredden.
Den lille firkant er 2,75m i længden og \(5m - 3m = 2m \) i bredden.
Herfra kan vi udregne arealet af de to, og lægge dem sammen:

$$ 7m \cdot 3m = 21m^2 \\
2.75m \cdot 2m =  5.5m^2 \\
21m^2 + 5.5m^2 = 26.5m^2 $$

Hvor mange gipsplader
Nu ganger vi væggenes areal med to, da der skal to lag gips på. Så lægger vi dette tal sammen med loftets areal. Hermed får vi antallet kvadratmeter, der skal gips på:

$$ 2\cdot 53.25m^2+26.5m^2 = 133m^2 $$

Husk at tage højde for spild
Vi ved, at en gipsplade er \( 2m^2 \). Derfor kan vi nu finde ud af, hvor mange gipsplader vi skal bruge. Vi mangler dog at tage højde for spild. I videoen fortæller Daniel, at selvom en gipsplade er \( 2m^2 \), regner de med, at man skal bruge to plader gips pr. kvadratmeter. Antallet af gipsplader til sådan en opgave, er derfor:

$$ 133m^2 \cdot 2\, \frac{\mathrm{gipsplader}}{m^2} = 266 \, \mathrm{gipsplader} $$

Hvor meget skal du slæbe frem og tilbage
Gipsplader vejer ca. \( 9 \frac{kg}{m^2} \), så ved \( 133m^2 \), hvor mange kilo gips skal man bære op i en lejlighed?
Vi laver udregningen 

$$ 133m^2 \cdot 9 \frac{kg}{m^2} = 1.197kg $$

Så man skal slæbe over et ton gips! Hvis Daniel havde lavet en fejl i sin udregning, kunne han risikere, at bære flere hundrede kilo gips op og ned fra en lejlighed.

Kilder:
https://www.jemogfix.dk/gipsplade-13-mm-90-x-240-cm/4132/9019243/