Påskeharer og Fibonacci

Nu er det snart påske, og hvis man er heldig, kommer påskeharen forbi med påskeæg. Traditionen om påskeharen er kun lidt over 100 år gammel. I begyndelsen af 1900-tallet kom traditionen fra Tyskland til Danmark. 

Traditionen har dog muligvis en førkristen oprindelse: Man har tidligere set haren som et frugtbarhedssymbol - og det samme gælder for æg, som derfor har indgået i frugtbarhedsritualer. At haren skulle være et frugtbarhedssymbol giver god mening: Dyr i harefamilien formerer sig nemlig rigtig hurtigt.

Vi har regnet ud, at hvis påskeharen kom til Danmark med en mage i år 1900, ville der i dag være \(1,45\cdot 10^{216}\) påskeharepar - forudsat at en påskehare lever evigt. 

Sådan har vi regnet det ud

Harebestande vokser enormt hurtigt, bl.a. fordi harer hurtigt bliver kønsmodne, og hunnerne er normalt kun drægtige i 41 dage.

Den måde, en kaninbestand udvikler sig på, blev undersøgt at den italienske matematiker Leonardo Fibonacci, og princippet er det samme for harer.

Før vi kan regne ud, hvor mange påskeharer, der er i Danmark i dag, skal vi først gøre et par antagelser:

• Vi starter med 1 harepar, nemlig Påskeharen og dens mage
• Tiden, det tager, før en hare bliver kønsmoden, sætter vi lig drægtighedstiden, nemlig 41 dage. De 41 dage udgør en periode.
• Vi antager, at der er to unger i hvert kuld
• Vi ser bort fra indavl
• Vi antager, at påskeharer tilhører en særlig hareart, som lever evigt

Lad os se på, hvordan bestanden af påskeharer udvikler sig fra år 1900 (starten på periode 1) og frem til begyndelsen af 6 periode:

Antal påbegyndte perioder	Antal påskeharepar	Forklaring
1	1	Ved start har vi 1 harepar, nemlig påskeharen og dens mage. De er endnu ikke kønsmodne. Vi kalder dette par for par nr. 1
2	1	Efter 41 dage har vi stadig kun 1 harepar, men Påskeharen og dens mage er nu blevet kønsmodne, og hunnen bliver drægtig.
3	2	Parret får nu et kuld unger, som vi kalder par nr. 2. Dette par er ikke kønsmodent, men hunnen i par 1 bliver drægtig igen.
4	3	Par nr. 1 får et kuld unger (par nr. 3) og hunnen bliver drægtig igen. Par nr. 2 er blevet kønsmodent, så hunnen i par 2 bliver drægtig.
5	5	Par nr. 1 får et kuld unger (par nr. 4), og hunnen bliver drægtig igen. Par nr. 2 får et kuld unger (par nr. 5), og hunnen bliver drægtig igen. Par nr. 3 er nu kønsmodent, så hunnen i parret bliver drægtig.
6	8	Par nr. 1 får et kuld unger (par nr. 6), og hunnen bliver drægtig igen. Par nr. 2 får et kuld unger (par nr. 7), og hunnen bliver drægtig igen. Par nr. 3 får et kuld unger (par nr. 8), og hunnen bliver drægtig igen. Par 4 og 5 er nu kønsmodne.

Udviklingen ses på billedet: 

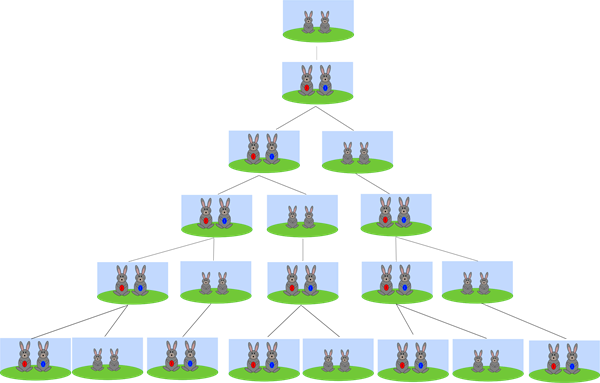
Lader man flere perioder gå, vil udviklingen fortsætte med 13, 21, 34, 55, 89 osv. harepar. Denne talrække er kendt som Fibonaccis talrække, hvor \(h _{n+2} = h_{n+1}+h_n\) . 

Man kan opstille en model, der beskriver denne udvikling: 

$$\mathrm{h(t)} = \frac{1}{\sqrt{5}} \cdot  \left( \left(\frac{1+\sqrt{5}}{2} \right)^t-\left( \frac{1-\sqrt{5}}{2} \right)^t \right)$$

Vi skal nu udregne, hvor mange perioder der er påbegyndt siden år 1900.

Antal år, der er gået: \(2016\mathrm{år}-1900\mathrm{år} = 116 \mathrm{år}\)

Dette gælder til og med år 2015.

Der er i gennemsnit 365,25 dage/år: \(116 \mathrm{år} \cdot 365,25 \mathrm{dage/år}= 42.369 \mathrm{dage}\)

I dag, torsdag d. 17/3, er der gået 77 dage af år 2016. I alt er der altså gået \( 42.369 \mathrm{dage} + 77 \mathrm{dage} = 42.446 \mathrm{dage} \)

Vi undersøger, hvor mange perioder på 41 dage, det svarer til:

$$ \frac{42.446 \mathrm{dage}}{41 \mathrm{dage/periode}} = 1035,27 \mathrm{perioder}$$

Der er altså påbegyndt 1036 perioder. Vi indsætter derfor 1036 i vores model:

$$\mathrm{h(1036)} = \frac{1}{\sqrt{5}} \cdot  \left( \left(\frac{1+\sqrt{5}}{2} \right)^{1036}-\left( \frac{1-\sqrt{5}}{2} \right)^{1036} \right) = 1,45\cdot 10^{216}$$

Vi ville altså have \(1,45\cdot 10^{216}\) påskeharepar i Danmark, hvis påskeharebestanden følger Fibonaccis model. 

Kilder:

http://madsenworld.dk/scripts/time-dk.htm

http://olewitthansen.dk/Matematik/Fibonacci.pdf

https://da.wikipedia.org/wiki/P%C3%A5skeharen

http://www.pattedyrforening.dk/soeg-viden/pattedyr/danske-ordener/harer-og-kaniner-lagomorpha