Etbarnspolitik i Kina
Siden 1979 har den kinesiske lov forhindret par i at få mere end ét barn for at undgå overbefolkning i Kina. Loven blev ophævet sidste år for at undgå en skævvridning i befolkningen med for få børn til at tage sig af de mange ældre - i 2014 faldt arbejdsstyrken med 3,7 millioner mennesker.
Efter der er blevet givet tilladelse til at få to børn, kunne man måske forvente en stor stigning i antallet af nyfødte børn, men der har ikke været - blandt andet fordi det er dyrt at få børn i Kina. Mange forældre fokuserer derfor på at give deres eneste barn de bedste forudsætninger for fx uddannelse.
Hvad var der sket, hvis Kina ikke havde haft en etbarnspolitik? Hvordan havde landet set ud i dag?
Den kinesiske stat mener selv, at der ville have været 400 millioner flere kinesere i dag, hvis det ikke havde været på grund at etbarnspolitikken, og det er selvfølgelig svært at modbevise den slags udtalelser om hypotetisk befolkningsudvikling. I stedet kan vi se på, hvordan andre lande, der er sammenlignelige med Kina, har udviklet sig demografisk.
Estimatet på 400 millioner bygger på forudsætningen om at befolkningsvæksten fra før etbarnspolitikken skulle fortsætte, men at denne vækst skulle være fortsat er ikke sandsynligt.
Generelt udvikler befolkningstal sig efter den logistiske vækstmodel:
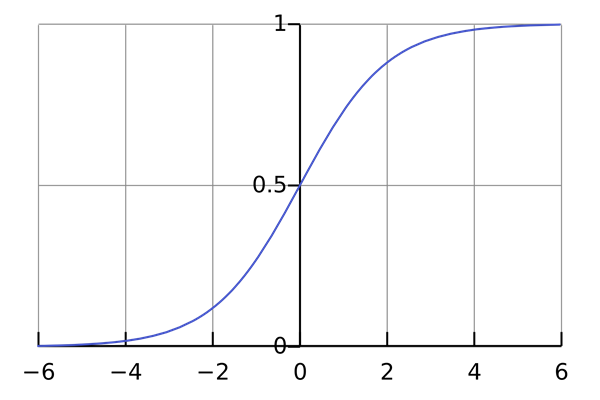
I den logistiske vækstmodel er grafen for funktionen først eksponentielt voksende og derefter ændrer den sig til at være eksponentielt aftagende. Der er nemlig et hæmmende led i forskriften for funktionen, og det får større og større betydning, jo større \(x\) bliver. Det betyder, at der er en øvre grænse for, hvor stor fx en bakteriekultur eller et befolkningstal kan blive. I praksis vil denne begrænsning være pga. mangel på mad eller fx højere forekomst af sygdomme, når man lever mange mennesker på lidt plads.
Funktionsforskriften for logistisk vækst er \(y(t)=\frac{\frac{b}{a}}{1+c\cdot e^{-bt}}\)
Det hæmmende led er \(\frac{b}{a}\), der også kaldes M. M er den øvre y-værdi for funktionen - funktionen vil være asymptotisk lig M, hvilket vil sige, at den kommer uendeligt tæt på, men aldrig helt når M.
Lad os se på, hvorfor M er den øvre grænse:
Hvis \(t \rightarrow \infty\) vil \( c \cdot e^{-bt}\) i funktionsforskriften
\(y(t)=\frac{\frac{b}{a}}{1+c\cdot e^{-bt}}\) gå mod 0. Derfor: Hvis vi lader t gå mod uendeligt, hvilket svarer til, at vi lader en befolkning udvikle sig i uendeligt mange år, vil nævneren gå mod 1, da leddet, der indeholder t, vil gå mod 0. Dermed vil funktionsforskriften gå mod \(\frac{1}{M}\), når x går mod \(\infty\).
At den kinesiske befolkningstilvækst skulle udvikle sig på samme måde som før etbarnspolitikken er derfor urealistisk, og der er ifølge flere eksperter nærmere et sted mellem 100 og 400 millioner kinesere mindre i dag, end der ville have været, hvis man ikke havde haft loven, der begrænsede antallet af børn.
Til gengæld har nogle forskere analyseret den kinesiske fødselsrate og sammenholdt den med udviklingen i andre lande. De har set på, hvordan udviklingen i Kina ville have været fra 1980'erne til 2010, hvis man ikke havde haft etbarnpolitikken. De konkluderer, at befolkningstallet ville have stabiliseret sig i løbet af perioden. Det ville medføre, at der i dag ville være omtrent samme antal kinesere, som vi ser i dag, men udviklingen ville bare have været mindre abrupt.
Kilder:
http://io9.gizmodo.com/did-chinas-one-child-policy-actually-reduce-population-1511784972
http://www.bbc.co.uk/schools/gcsebitesize/geography/population/managing_population_rev3.shtml
https://en.wikipedia.org/wiki/Demographics_of_China
https://en.wikipedia.org/wiki/One-child_policy
