Monty Hall-problemet
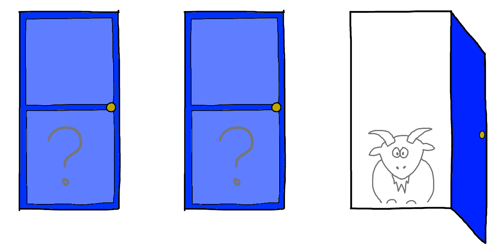
Antag, at du er med i et tv-program, hvor du får muligheden for at vælge mellem tre døre. Spilstyreren har gemt en bil bag en af dørene, og en ged bag hver af de to andre. Spilstyreren siger: "Først vælger du en dør, og så åbner jeg en af de to andre døre, bag hvilken der er en ged. Efter jeg har åbnet en dør med en ged bag, tager du dit endelige valg. Du kan holde på den dør, du valgte til at starte med, eller du kan vælge om og tage den sidste dør. Du vinder det, der er bag den dør du vælger."
Lad os sige, at du starter med at vælge dør 1. Spilstyreren åbner nu dør 3, og viser en ged. Er der nu en fordel at vælge om, og tage dør nummer 2 i stedet?
Dette problem kaldes Monty Hall-problemet, opkaldt efter den amerikanske TV-vært Monty Hall, der havde et program med et lignende dilemma. Hvis du vil prøve at løse problemet selv, så læs ikke videre - løsningen kommer nemlig nu.
Løsning
Siden tv-værten har åbnet en dør med en ged bag, er der nu én tilbage med en bil, og én med en ged. Det leder mange til at tro, at sandsynligheden for at bilen er bag døren er lige stor for de to resterende døre. Men det viser sig faktisk at være en fordel at skifte dør. Hvis du gør det, vinder du nemlig bilen i to ud af tre tilfælde. Det vil altså sige, at der er dobbelt så stor sandsynlighed for at vinde bilen, hvis du vælger om.
Grunden til dette ligger i, at det ikke er tilfældigt, hvilken dør værten åbner. Han vil altid åbne en dør med en ged bag. Hvis du har valgt bilen i første omgang, hvilket der er 1/3 sandsynlighed for, vil der altså være en ged bag døren hvis du vælger om. Men hvis du derimod har valgt en ged fra starten af, hvilket der er 2/3 sandsynlighed for, er spilstyreren nødt til at afsløre den anden ged, og et omvalg vil resultere i at du vinder bilen.
Vi kan dele dette op i tre situationer:
- Du starter med at vælge den ene ged, lad os kalde den Ged A
- Du starter med at vælge den anden ged, lad os kalde den Ged B
- Du starter med at vælge bilen
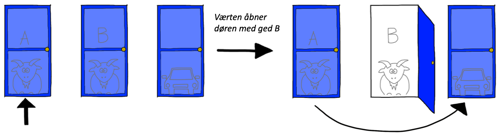
I den første situation, har du til at starte med valgt Ged A. Spilstyreren åbner døren med Ged B bag, og du vinder bilen ved at skifte dør.
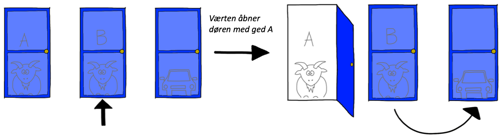
I den anden situation vælger du døren med Ged B til at starte med. Et skift til den anden dør gør igen, at du vinder bilen.
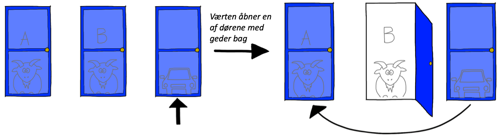
I den tredje situation har du til at starte med valgt døre, der skjuler bilen. Spilstyreren åbner en dør med en af gederne bag, og du vinder ikke bilen ved at skifte dør.
Problemets løsning bygger på kombinatorik og sandsynlighedsregning. Alligevel er det så kontraintuitivt, at mange har svært ved at acceptere det. Da Marilyn vos Savant gav løsningen til dette problem i magasinet Parade, var der tusinder af folk der skrev ind til hende, at hun tog fejl. Herunder flere hundrede matematikprofessorer. Men hun tog ikke fejl, det passer ganske rigtigt, at du har dobbelt så stor chance for gevinst, hvis du vælger om til sidst.
