Feriedestination London
Rigtig mange danskere rejser hvert år til storbyer som Paris, Barcelona og London.
Matematikcenter har set nærmere på, hvor der er matematik i disse feriedestinationer, så du har nogle funfacts at imponere familien eller vennerne med på turen.
Vidste du for eksempel, at franske matematikeres navne er indgraveret i Eiffeltårnet, og at Sagrada Familias lysskakter er udformet som hyperboloider? Eller at tiden går en lillebitte smule hurtigere, når du er oppe i London Eye?
London
I London findes London Eye, der er et stort pariserhjul ved Themsen. En tur rundt i hjulet tager 30 minutter, og diameteren af hjulet er 120 m.
På grund af Einsteins generelle relativitetsteori går tiden ikke lige hurtigt alle steder. Tiden går nemlig langsomt, når man er tæt på tunge objekter som fx jorden.
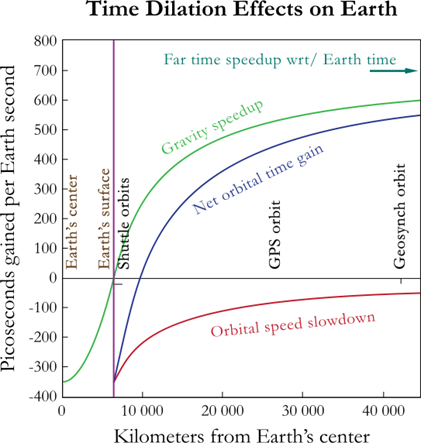
Derfor går tiden en lille smule hurtigere, når man er oppe i toppen af London Eye. Vi udregner, hvor meget hurtigere tiden går oppe i pariserhjulet ved hjælp af denne tilnærmede formel, der er et af de mange resultater af Einsteins generelle relativitetsteori:
$$\frac{T_{nede}}{T_{oppe}}\approx 1+ \frac{gh}{c^2}$$
\(T_{nede}\) er tiden, det tager for et ur i bunden af London Eye at sige "tik", mens \(T_{oppe}\) er tiden, det tager for et ur i toppen af London Eye at sige "tik".

Vi finder altså forholdet mellem de to tider. \(g\) er størrelsen af tyngdeaccelerationen (9,82 m/s\(^2\)), mens \(h\) er højden (120 m). \(c\) er lysets hastighed, som vi sætter til \(3\cdot 10^8\) m/s.
Vi indsætter vores værdier:
$$\frac{T_{nede}}{T_{oppe}}\approx 1+ \frac{9,82\,\mathrm{m/s}\cdot 120\,\mathrm{m}}{(3\cdot10^8 \,\mathrm{m/s})^2}=1,000000000000013093$$
Det vil sige, at forholdet mellem tiden nede og tiden oppe i London Eye er 1,000000000000013093. Vi kan gange med \(T_{oppe}\) på begge sider:
$$\frac{T_{nede}}{T_{oppe}}\approx1,000000000000013093 \Leftrightarrow T_{nede} \approx1,000000000000013093\cdot T_{oppe}$$
Hver gang der går et sekund nede, går der altså 1,000000000000013093 sekunder oppe i toppen af London Eye. Der er altså en forskel ude på det 14. decimal, og man skal derfor vente et godt stykke tid oppe i London Eye, før man bliver et helt sekund ældre end man ville have været, hvis man stod på jorden.
Kilder
https://en.wikipedia.org/wiki/Eiffel_Tower
https://en.wikipedia.org/wiki/List_of_the_72_names_on_the_Eiffel_Tower
http://www.sagradafamilia.org/en/geometry/
https://da.wikipedia.org/wiki/Massefylde
https://en.wikipedia.org/wiki/Sagrada_Fam%C3%ADlia
http://mimimi.dk/bcn/ivan/Barcelona_kursus_sept_2010/Gaudi_geometri_09.pdf
https://en.wikipedia.org/wiki/London_Eye
"Gaudis arkitektur med TI-Nspire CAS" af Bjørn Felsager, 2013
"Physical Mathematics" af Kevin Cahill, 2013
