Fibonacci-julekalender
Følg med i vores julekalender hver dag på vores facebook-side. Julekalenderen følger i år Fibonacci-tallene, og et nyt afsnit bliver offentliggjort de dage i december, der matcher et Fibonacci-tal. I hvert afsnit præsenterer vi en lille opgave, som I kan løse, tage et billede af, uploade i kommentarsporet, og være med i vores december-konkurrence.
Til hver opgave vil vi her på siden komme med en gennemgang af de informationer, der er nødvendige til at løse opgaven.
Første december, anden december, tredje december, femte december, ottende december, 13. december, 21. december.
1. december
Velkommen til vores julekalender her på Matematikcenter. I dag den første december er der to afsnit: ét, hvor vi præsenterer julekalenderen, og et om kalenderlys' brændetid.
Opgaven består i, at du måler radius og højden på dit eget kalenderlys og sætte de værdier ind i de formler vi har fået. Nedenfor er et billede af regressionslinjen og formlen, som vi også viste i kalender-afsnittet.
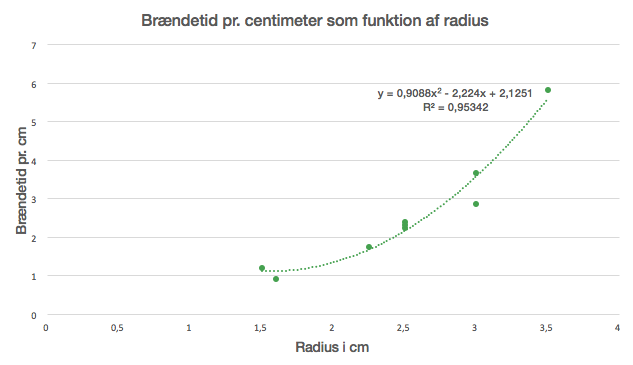
Brændetiden, \(T_{cm}\) i timer pr. cm som funktion af radius i cm, \(r\), kan altså findes ud fra følgende funktion:
\(T_{cm}=0,9088 \cdot r^2 - 2,224 \cdot r + 2,1251\)
Når brændetiden i timer pr. cm er fundet, så kan dette ganges med lysets højde i cm, \(h\) for at finde den samelde brændetid, \(T_{total}\).
\(T_{total} = T_{cm} \cdot h\)
Video 1:
Video 2:
2. december
Her den anden december stiller vi spørgsmålet: er der en sammenhæng mellem bredden på strimler brugt til at lave musetrapper med, og deres længde når de er helt strukket ud?
I videoen laver vi tre forskellige musetrapper af strimler med en bredde på hhv. 1, 2 og 4 cm. Allestrimlerne er lavet af den lange side af et A4-papir, og er altså 29,7 cm lange. Da vi målte vi musetrappen med en strimmel-bredde på 2 cm, fandt vi dens længde til at være 17 cm.
Som en sidste info tager resultatet vi har fundet ikke højde for de små variationer, der automatisk vil opstå i klipningen og foldningen af musetrapperne.
Video:
3. december
Dagens afsnit af Matematikcenters julekalender handler om matematisk julepynt. Vi har taget udgangspunkt i de platoniske legemer, som vi har lavet klippe-klistre-skabeloner ud af.
Platoniske legemer er en særlig klasse af figurer, der opfylder en række krav. De skal bl.a. være opbygget af ens ligesidede polygoner, og have lige mange sider der mødes ved hvert hjørne.
I de tre dimensioner vi møder i dagligdagen er der kun fem af sådanne former, men i højere dimensioner stiger antallet af mulige legemer.
De fem vi har lavet til julepynt hedder tetraede (fire sider), kube (seks sider), oktaede (otte sider), dodekaede (12 sider) og ikosaede (20 sider).
Video:
5. december
I dag handler julekalenderen om fraktaler; nærmere bestemt Von Kochs snefnug. Hvordan denne er defineret er bedst forklaret i videoen, men opgaven vi stiller handler om dens areal og omkreds. Hver af siderne i trekanten \(S_0\) har længden 20 cm, og længden af hver af disse er efter et givet antal iterationer, \(n\), givet ved \(\frac{4}{3}^n\).
Det snefnug vi endte med var den tredje-iteration, og omkredsen er derfor til at regne ud.
Et lidt sværere spørgsmål er udregningen af vores snefnugs areal. Det er dog overkommeligt, hvis man kender formlen for arealet af en trekant \(A_{trekant}=\frac{g \cdot h}{2}\), hvor \(h\) og \(g\) er trekantenst højde og grundlinje, og ved at, hver af de nye trekanter har en sidelængde svarende til en tredjedel af den foregående.
Video:
8. december
Her den ottende december handler vores julekalender om kræmmerhuse; nærmere bestemt, det optimale kræmmerhus. Med det menes ikke det pæneste kræmmerhus (det er jo en personlig vurdering), men det kræmmerhus med det største rumfang.
Læs mere om: optimering
Vi har taget udgangspunkt i et almindeligt A4-papir, ud af hvilket der klippes en cirkel. Cirklens radius er lig halvdelen af papirets bredde og er \(\frac{210\ mm}{2}=105\ mm\). Et kræmmerhus har samme form som en kegle, hvis rumfang er givet ved \(V_{kegle} = \frac{1}{3} \cdot \pi \cdot h \cdot r^2\), hvor \(h\) er kræmmerhusets højde og \(r\) er radius i den cirkel, som er kræmmerhusets åbning.
Ud fra pythagoras kan vi finde følgende sammenhæng mellem \(r\) og \(h\): \((105\ mm)^2 = r^2 + h^2\), hvilket kan omskrives til \(r(h) = \sqrt{(105\ mm)^2 + h^2}\). Denne funktion \(r(h)\) indsættes i formlen for rumfanget, der nu kun har én variabel, \(h\). \(V_{kegle}(h) = \frac{1}{3} \cdot \pi \cdot h \cdot r(h)^2 = 3675 \cdot h \cdot \pi - \frac{h^3 \cdot \pi}{3}\).
Dette udtryk kan herefter differentieres for at finde den højde, \(h\), der giver det største rumfang.
\(V_{kegle}'(h) = 3675 \cdot \pi - \pi \cdot h^2\)
\(115,45 - \pi \cdot h^2 = 0\)
\(60,6\ mm = h\)
Den værdi for højden sætter vi ind i udtrykket for radius i kræmmerhusets åbning for at finde omkredsen af åbningen, hvilket divideres med omkredsen af vores oprindelige cirkel. Dette giver os den andel af cirklen vi skal bruge for at lave kræmmerhuset
\(\frac{2 \cdot \pi \cdot r(60,6 mm)}{2 \cdot \pi \cdot 105\ mm} = 81,7 \%\)
På skabelonen er et udsnit på \((100 \% - 81,7 \%) \cdot 360° = 65,88°\) markeret.
Video:
13. december
Her på Lucia dag handler vores julekalender om den geometriske figur Möbiusbåndet. Det særlige ved denne figur er, at det modsat f.eks. en normal papirring kun har én side og én flade - et bånd har to af hver. Man laver et Möbiusbånd ligesom man ville lave normale guilanderinge, bortset fra, at man drejer den ene ende af papirstrimlen 180° inden man taper det sammen med den anden endne.
Möbiusbåndet derfor en række egenskaber, der adskiller det fra normale bånd, særligt hvis man klipper det over. Et eksempel herpå er, at et Möbius får en ekstra snoning, hvis man klipper det over langs midten af båndet. En anden egenskab er, at man kan lave to Möbiusbånd om til to hjerter, hvad vi gør i afsnittet. Dette kræver lidt snilde, men det vigtigeste er at huske på, at de to bånd skal sno i hver sin retning.
Video:
