Matematikcenters frivillige
Hvis du har brugt Matematikcenters lektiecaféer, har du mødt nogle af vores mange dygtige frivillige. Men hvem er de egentlig, og hvordan ser de sig selv i lektiecaféerne?
Vi har lavet lidt statistik på den evaluering, som vores frivillige har besvaret i år. De frivillige er meget forskellige, og nogen er nye i organisationen, mens andre har været frivillige i flere år. Alligevel har de nogle ting til fælles. Blandt andet ser de sig selv som tålmodige, venlige og imødekommende, og mere end 94 % af dem er enige eller delvist enige i, at de viser eleverne nye måder at forstå matematikken på.

Hvor længe har de frivillige været hos Matematikcenter?
40 frivillige svarede på den seneste frivilligevaluering. Vi regner ud, hvor længe de frivillige gennemsnitligt har været tilknyttet Matematikcenter. Datasættet ser ud som følger (angivet i måneder):
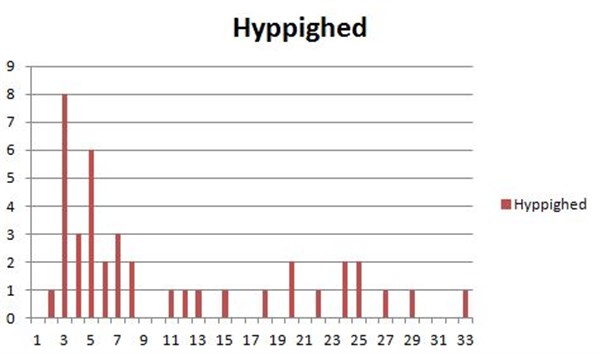
2,3,3,3,3,3,3,3,3,4,4,4,5,5,5,5,5,5,6,6,7,7,7,8,8,11,12,13,15,18,20,20,22,24,24,25,
25,27,29 og 33.
Her ses data afbildet som histogram:
Middelværdien \(\overline{x}\) findes med formlen
$$\overline{x}=\frac{1}{n}\cdot \sum_{i=1}^kh_i \cdot x_i=\frac{h_1\cdot x_1+h_2\cdot x_2+...+h_k\cdot x_k}{n}$$
n er størrelsen af populationen (40 frivillige), k er antallet af forskellige tilknytningstider (19) og h er hyppigheden for hver af de 19 tilknytningstider.
Middelværdien udregnes som:
$$\frac{2\mathrm{md.}+8\cdot 3\mathrm{md.}+3 \cdot 4\mathrm{md.}+6\cdot 5 \mathrm{md.}+2 \cdot 6 \mathrm{md.}+\\3 \cdot 7 \mathrm{md.}+2 \cdot 8\mathrm{md.} + 11 \mathrm{md.}+ 12 \mathrm{md.}+13\mathrm{md.}+\\15\mathrm{md.}+18\mathrm{md.}+2\cdot 20 \mathrm{md.}+ 22\mathrm{md.}+\\2\cdot 24 \mathrm{md.}+2\cdot 25 \mathrm{md.}+27\mathrm{md.}+29\mathrm{md.}+33\mathrm{md.}}{40 \mathrm{frivillige}} = 10,875 \mathrm{md./frivillig}$$
Vi kan finde variansen for datasættet ved at bruge formlen
$$\mathrm{Var}(x)=\frac{1}{n-1}\sum_{i=1}^kh_i(x_i-\overline{x})^2= \frac{h_1(x_1-\overline{x})^2+h_2(x_2-\overline{x})^2+...+h_k(x_k-\overline{x})^2}{n-1}$$
Man dividerer med n-1, da det ikke er givet, at data er fordelt efter fx normalfordelingen.
Udtrykket ser altså sådan ud ((\(x\) og \(\overline{x}\) har enheden måned):
$$ \mathrm{Var}(x) =\frac{(2-10,875)^2+8(3-10,875)^2+3(4-10,875)^2\\+6(5-10,875)^2+2(6-10,875)+3(7-10,875)^2\\+2(8-10,875)^2+(11-10,875)^2+(12-10,875)^2\\+(13-10,875)^2+(15-10,875)^2+(18-10,875)^2\\+2(20-10,875)^2+(22-10,875)^2+2(24-10,875)^2\\+2(25-10,875)^2+(27-10,875)^2+2(29-10,875)^2\\+(33-10,875)^2}{40-1}\\ \qquad \qquad=82,52$$
Variansen har enheden \(\mathrm{måned}^2\).Der er altså stor varians ift. hvor længe de frivillige har været tilknyttet matematikcenter.
Vi kan beregne spredningen/standardafvigelsen med \(\sigma(x)=\sqrt{\mathrm{Var}(x)}\):
$$\sigma(x)=\sqrt{82,52}=9,08 \mathrm{md.}$$
Vi er rigtig glade for at have så mange nye frivillige, samtidig med at vi har nogle frivillige, der har været i organisationen i flere år.

Hvordan beskriver de frivillige sig selv?
Vi bad de frivillige beskrive, hvad der kendetegner dem som frivillige i Matematikcenter med tre tillægsord, og \(\frac{17 }{40}\) beskrev sig som imødekommende og \(\frac{19}{40} \) beskrev sig som tålmodige. Det er hhv. \(\frac{17 \mathrm{frivillige}}{40\mathrm{frivillige}}\cdot100\%=42,5\%\) og \(\frac{19 \mathrm{frivillige}}{40\mathrm{frivillige}} \cdot100\%=47,5\%\)
Herudover bliver ord som venlig og hjælpsom brugt ofte, mens andre beskriver sig som fx lyttende, humoristiske, engagerede, kompetence, vedholdende og glade.

De frivillige er altså enige om, at de bidrager med en masse positive elementer, og de er derfor med til at skabe et godt læringsmiljø i lektiecaféerne.
Viser de eleverne nye måder at forstå matematik på?
18 ud af de 37 frivillige (3 besvarede ikke dette spørgsmål) er enige i, at de viser eleverne nye måder at forstå matematik på, og 17 er delvist enige. I alt giver det:
$$\frac{18 \mathrm{frivillige}+17 \mathrm{frivillige}}{40 \mathrm{frivillige}}\cdot 100\%=94,6\%$$

Konklusion
Hvis du kommer i Matematikcenters lektiecaféer, vil du møde nye frivillige og frivillige, der har været længe i Matematikcenter. De mener alle sammen, at de bidrager til at du forstår matematik på en ny måde og at det er rart at lære matematik, blandt andet fordi de er imødekommende og tålmodige.
Har du en god oplevelse fra en af Matematikcenters lektiecaféer?
Så er du velkommen til at dele den med os på Facebook.
